chapter09 方差分析
文章目录
方差分析
- 当包含的因子是解释变量时,我们关注的重点通常会从预测转向组别差异的分析,这种分析法称作方差分析 (ANOVA)。
1、术语
- 均衡/非均衡设计:不同观测方案的观测数相同/不同
- 单因素方差分析:仅有一个类别型变量,一般为组间两水平因子(两种药物)
- 单因素组内方差分析:仅有一个类型形变量,一般为组内两水平因子(同种药物,作用时间不同)
- 因素方差分析:设计包含两个甚至更多的因子
- 混合模型方差分析:因子设计包括组内和组间因子
- 混淆因素/干扰因子:你不关心的因素,但其能解释你关心的组间差异
- 协方差分析(ANCOVA):度量并将混淆因子作为协变量考虑在模型中的方差分析
- 多元方差分析(MANOVA):因变量不止一个
- 多元协方差分析(MANCOVA):因变量不止一个的协方差分析
2、ANOVA模型拟合
|
|
一些常见的研究设计表达式:
|
|
2.2、顺序很重要
- 例如,对于双因素方差分析,不同的处理方式观测数不同,则y~AB与y~BA结果不同
假设你正使用如下表达式对数据进行建模:
- Y ~ A + B + A:B
有三种类型的方法可以分解等式右边各效应对y所解释的方差。
- 类型I(序贯型):效应根据表达式中先出现的效应做调整。 A不做调整, B根据A调整, A:B交互项根据A和B调整。
- 类型II(分层型):效应根据同水平或低水平的效应做调整。 A根据B调整, B依据A调整,A:B交互项同时根据A和B调整。
- 类型III(边界型):每个效应根据模型其他各效应做相应调整。 A根据B和A:B做调整, A:B交互项根据A和B调整。
样本大小越不平衡,效应项的顺序对结果的影响越大。一般来说,越基础性的效应越需要放在表达式前面。具体来讲,首先是协变量,然后是主效应,接着是双因素的交互项,再接着是三因素的交互项,以此类推。
- R默认调用类型I方法,其他软件(比如SAS和SPSS)默认调用类型III方法。
- car包中的Anova()函数(不要与标准anova()函数混淆)提供了使用类型II或类型III方法的选项。
3、单因素方差分析
|
|

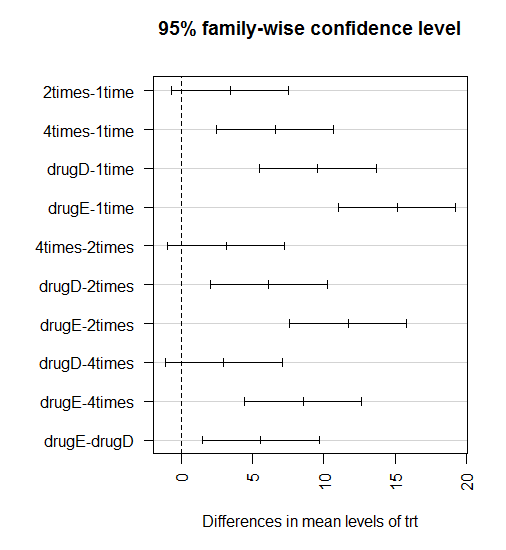
3.1、多重比较
|
|
|
|
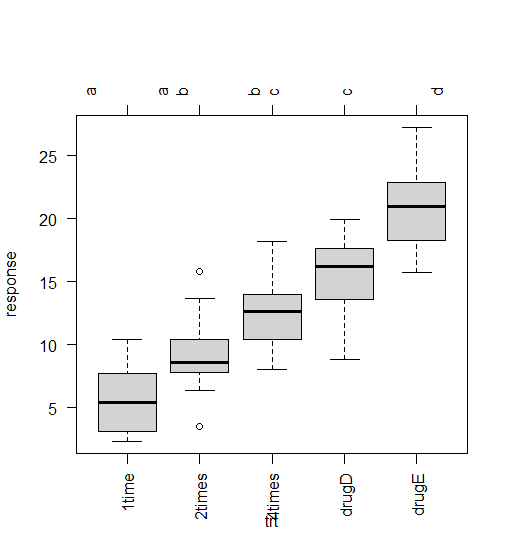
3.2、检验的假设条件
- 样本随机独立
- 因变量的正态性
|
|
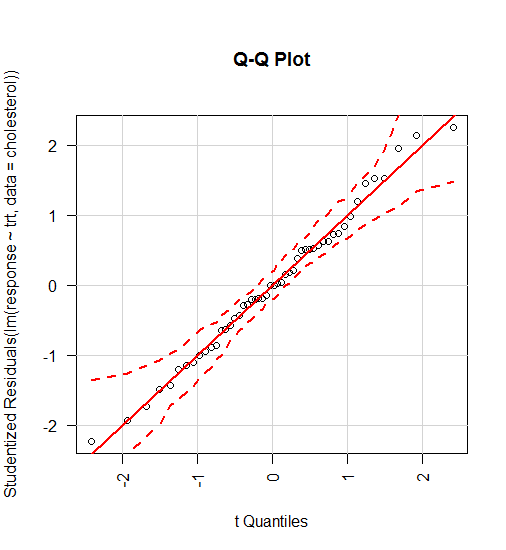
- 样本的方差齐性(总体方差相等)
注意:F检验对于数据的正态性非常敏感,因此在检验方差齐性的时候,Levene检验, Bartlett检验或者Brown–Forsythe检验的稳健性都要优于F检验。 F检验还可以用于三组或者多组之间的均值比较,但是如果被检验的数据无法满足均是正态分布的条件时,该数据的稳健型会大打折扣,特别是当显著性水平比较低时。但是,如果数据符合正态分布,而且alpha值至少为0.05,该检验的稳健型还是相当可靠的。
|
|
4、协方差分析
|
|
4.1、检验的假设条件
|
|
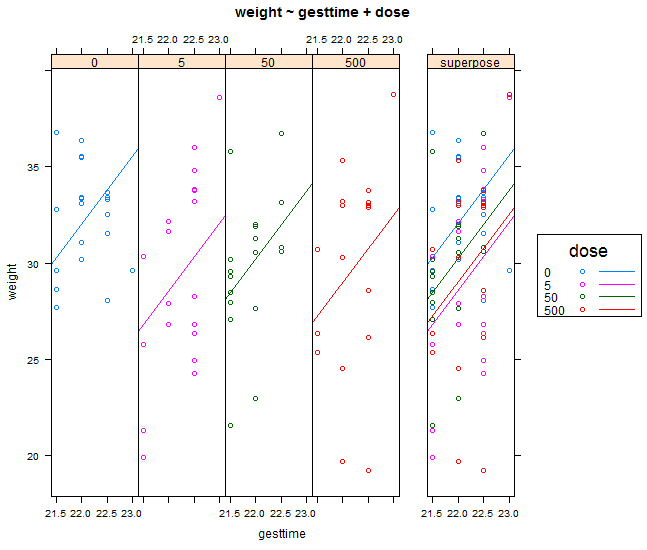
4.2、可视化
|
|
5、双因素方差分析
|
|
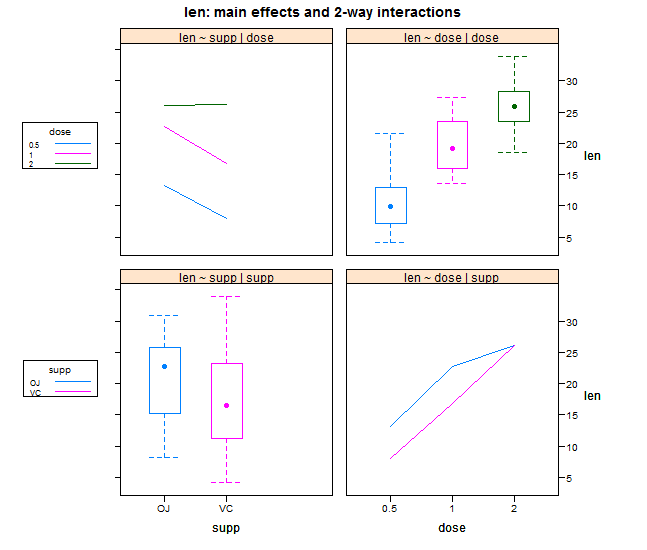
6、重复测量方差分析
|
|
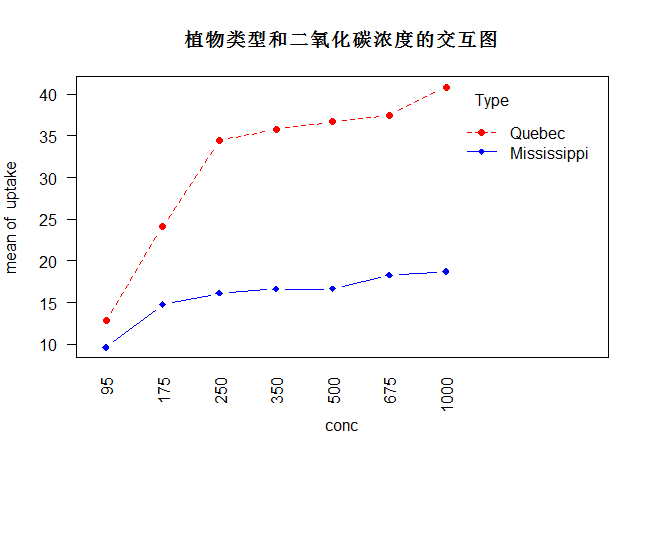

7、多元方差分析
|
|
7.1、评估假设检验
- 多元正太性
|
|
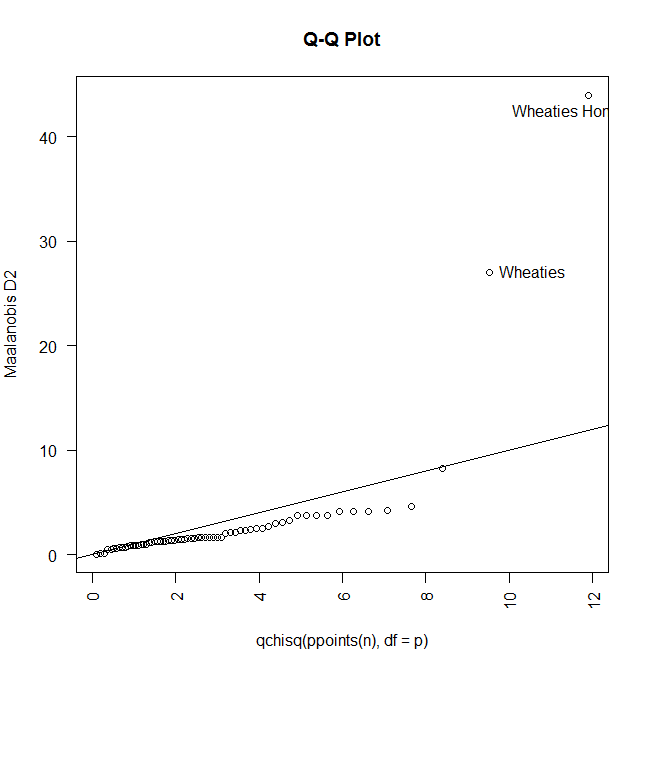
方差-协方差矩阵同质性
暂时没找到合适的方法来进行检验
多元离群点
12library(mvoutlier)aq.plot(y)
7.2、稳健多元方差分析
- 多元正态性或方差-协方差同质性不满足或担心离群点时
- rrcov包中Wilks.test(y.dataframe,x,method=”mcp”)
- vegan包中的adonis()12345678910#稳健多元方差分析library(MASS)attach(UScereal)#稳健多元单因素方差分析library(rrcov)y<-cbind(calories,fat,sugars)Wilks.test(y,shelf,method="mcd")#性能较慢#非参数多元方差分析library(vegan)adonis(y~shelf)
8、用回归做ANOVA
- 当lm()函数碰到因子时,它会用一系列与因子水平相对应的数值型对照变量来代替因子。(s1,s2,s3=>(0,0,0),(0,1,0),(0,0,1))
| 创建方法 | 描述 |
|---|---|
| contr.helmert | 第二个水平对照第一个水平,第三个水平对照前两个的均值,第四个水平对照前三个的均值,以此类推 |
| contr.poly | 基于正交多项式的对照,用于趋势分析(线性、二次、三次等)和等距水平的有序因子 |
| contr.sum | 对照变量之和限制为0。也称作偏差找对,对各水平的均值与所有水平的均值进行比较 |
| contr.treatment | 各水平对照基线水平(默认第一个水平)。也称作虚拟编码 |
| contr.SAS | 类似于contr.treatment,只是基线水平变成了最后一个水平。生成的系数类似于大部分SAS过程中使用的对照变量 |
- fit.lm <- lm(response ~ trt, data=cholesterol, contrasts=”contr.SAS”)的contrasts参数来改变创建方法,默认的创建方法为contr.treatment) 1234567891011121314151617181920212223242526272829303132333435> ##使用回归进行方差分析> library(multcomp)> levels(cholesterol$trt)[1] "1time" "2times" "4times" "drugD" "drugE"> fit.aov <- aov(response ~ trt, data=cholesterol)> summary(fit.aov)Df Sum Sq Mean Sq F value Pr(>F)trt 4 1351.4 337.8 32.43 9.82e-13 ***Residuals 45 468.8 10.4---Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1>> fit.lm <- lm(response ~ trt, data=cholesterol)> summary(fit.lm) #二者一致Call:lm(formula = response ~ trt, data = cholesterol)Residuals:Min 1Q Median 3Q Max-6.5418 -1.9672 -0.0016 1.8901 6.6008Coefficients:Estimate Std. Error t value Pr(>|t|)(Intercept) 5.782 1.021 5.665 9.78e-07 ***trt2times 3.443 1.443 2.385 0.0213 *trt4times 6.593 1.443 4.568 3.82e-05 ***trtdrugD 9.579 1.443 6.637 3.53e-08 ***trtdrugE 15.166 1.443 10.507 1.08e-13 ***---Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1Residual standard error: 3.227 on 45 degrees of freedomMultiple R-squared: 0.7425, Adjusted R-squared: 0.7196F-statistic: 32.43 on 4 and 45 DF, p-value: 9.819e-13

