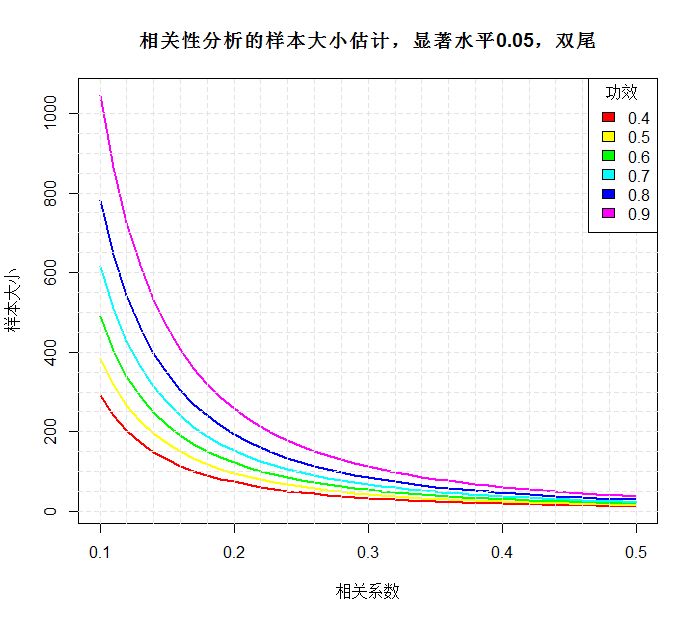
library(pwr) r<-seq(0.1,0.5,0.01) nr<-length(r) p<-seq(0.4,0.9,0.1) np<-length(p) samsize<-array(numeric(nr*np),dim=c(nr,np)) for(i in 1:np){ for(j in 1:nr){ result <- pwr.r.test(n=NULL,r=r[j],sig.level = 0.05,power=p[i],alternative = "two.side") samsize[j,i]<-ceiling(result$n) } } xrange<-range(r) yrange<-round(range(samsize)) colors<-rainbow(length(p)) plot(xrange,yrange,type="n",xlab="相关系数",ylab="样本大小") for(i in 1:np){ lines(r,samsize[,i],type="l",lwd=2,col=colors[i]) } abline(v=0,h=seq(0,yrange[2],50),lty=2,col="grey89") abline(h=0,v=seq(xrange[1],xrange[2],0.02),lty=2,col="grey89") title("相关性分析的样本大小估计,显著水平0.05,双尾") legend("topright",title="功效",as.character(p),fill = colors)
|