chapter11 中级绘图
中级绘图
1、散点图
|
|
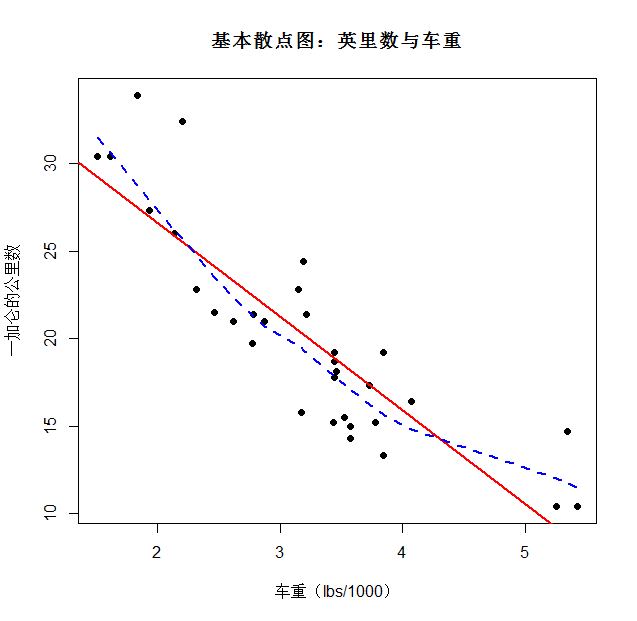
|
|
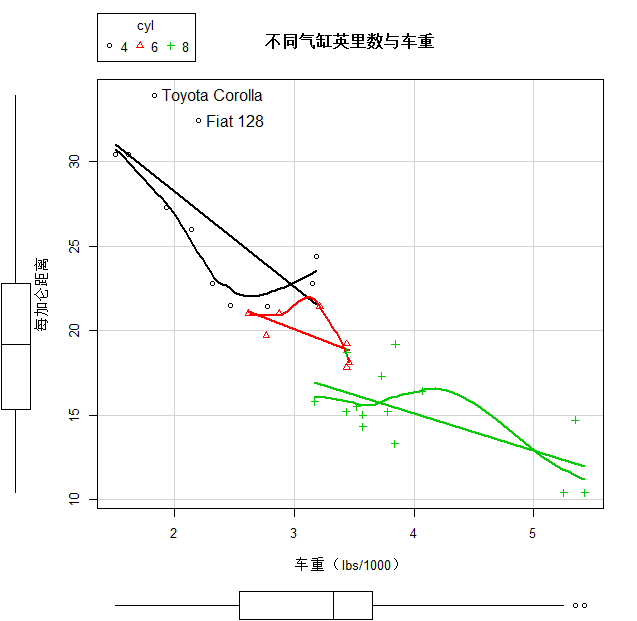
1.1、散点矩阵图
|
|

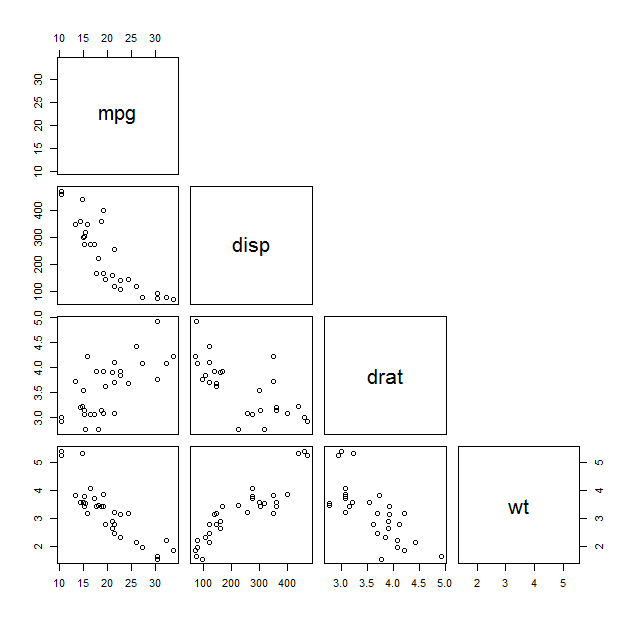
|
|
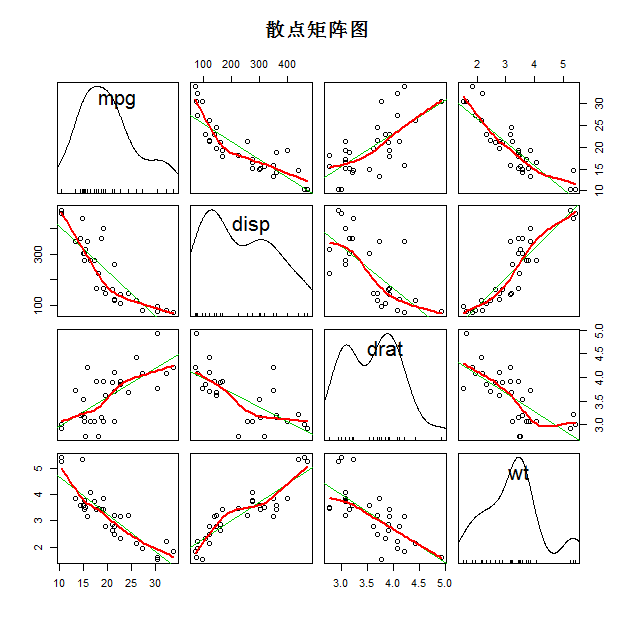
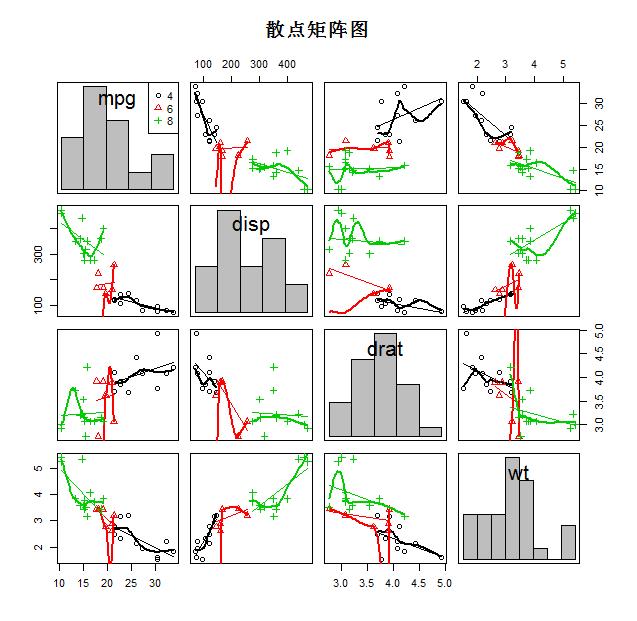
|
|
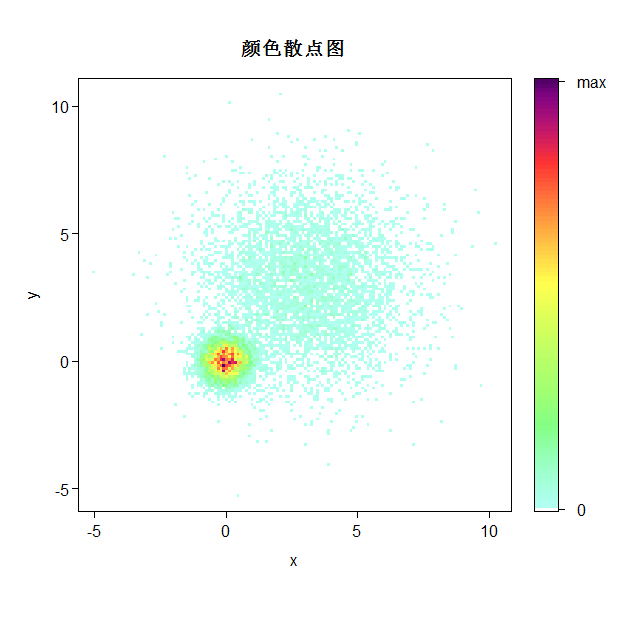
1.2、高密度散点图
|
|
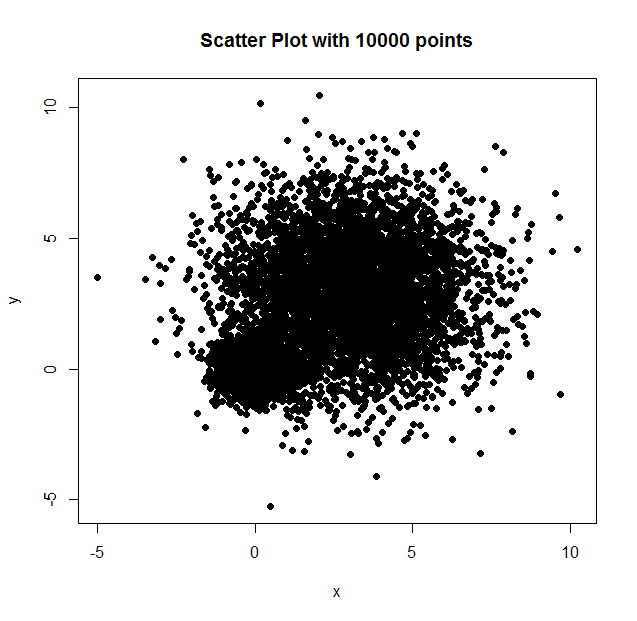
|
|
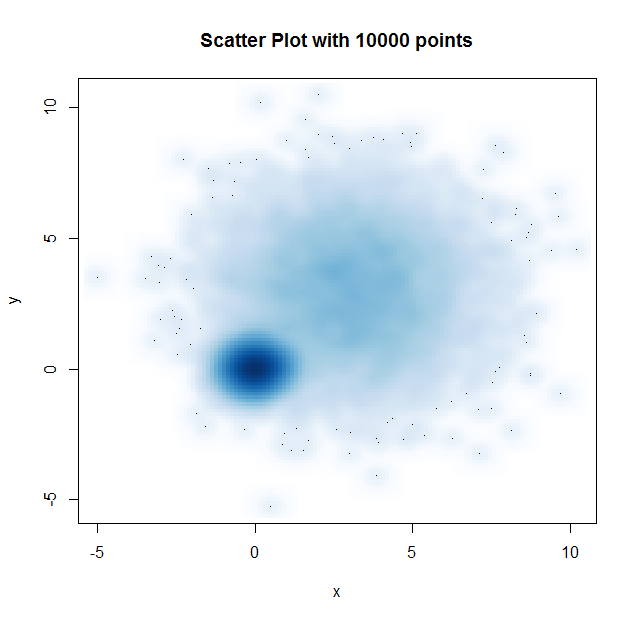
|
|

|
|
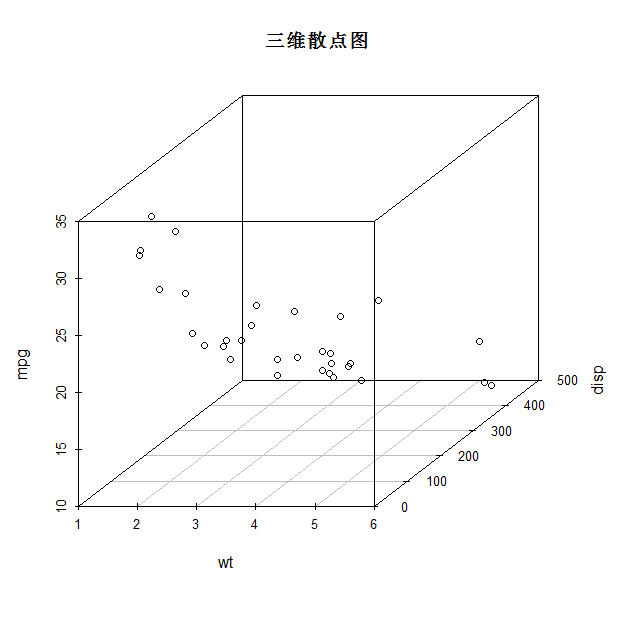
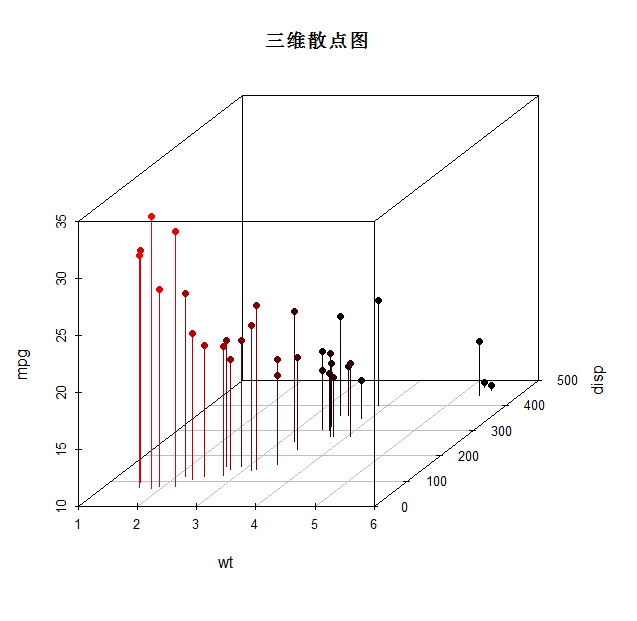
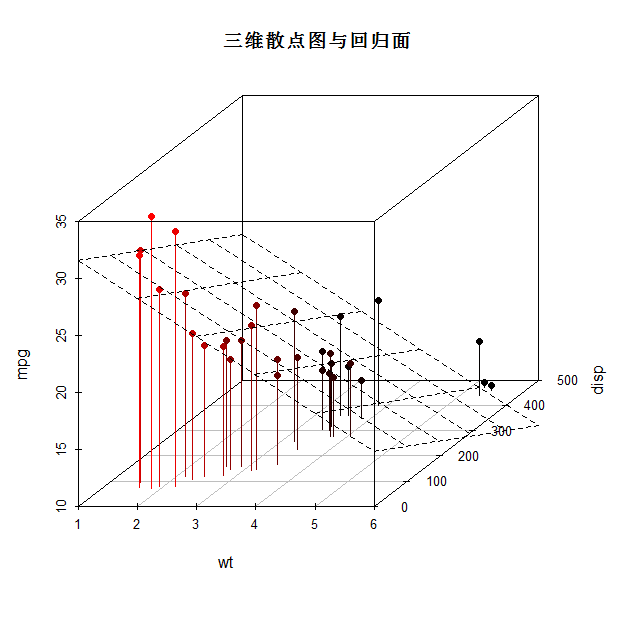
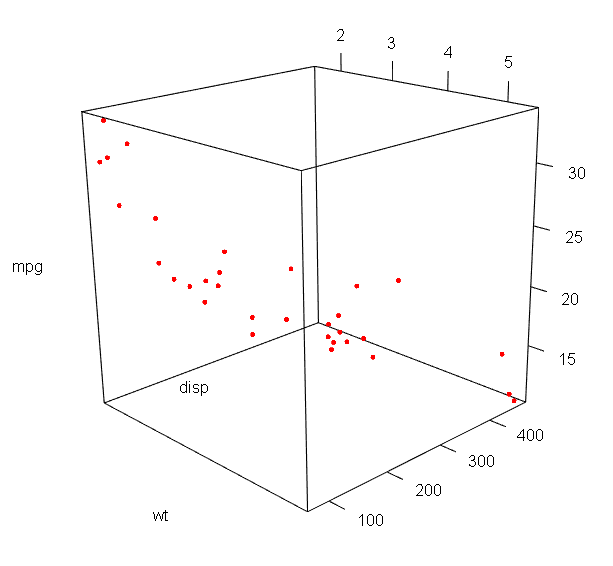
1.3、三维散点图
|
|
|
|
|
|
|
|
|
|

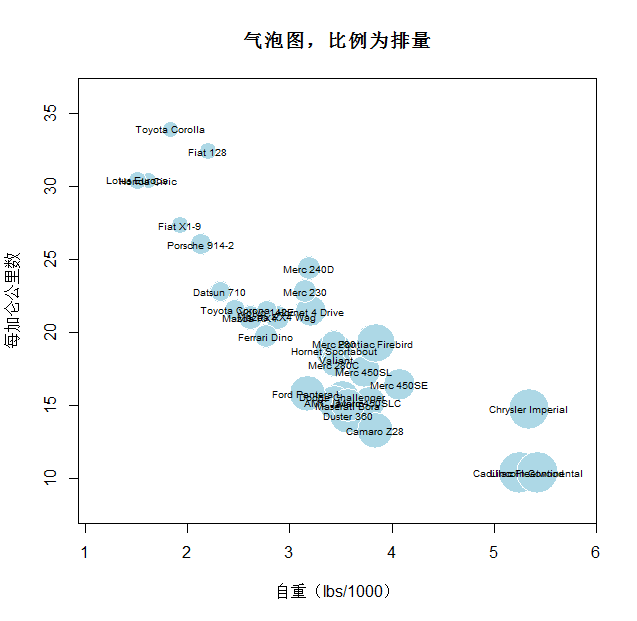
1.4、气泡图
|
|
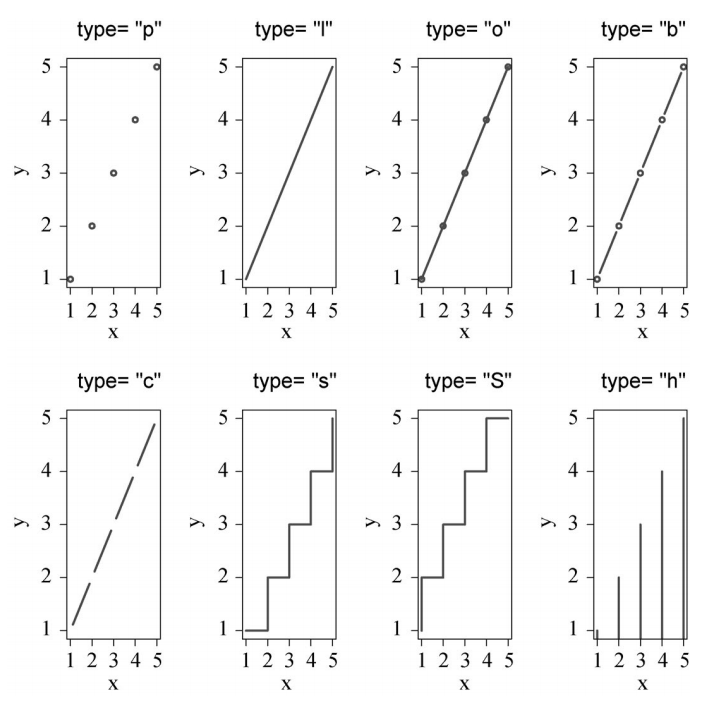
2、折线图
- 大多数内容第三章已经说明

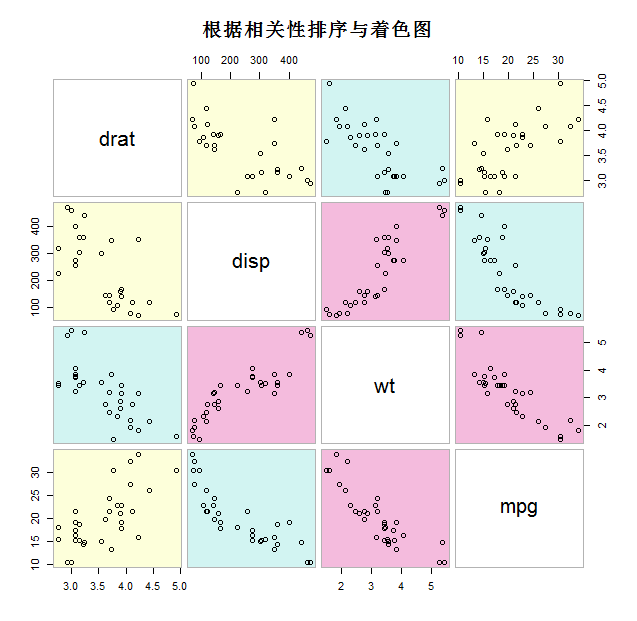
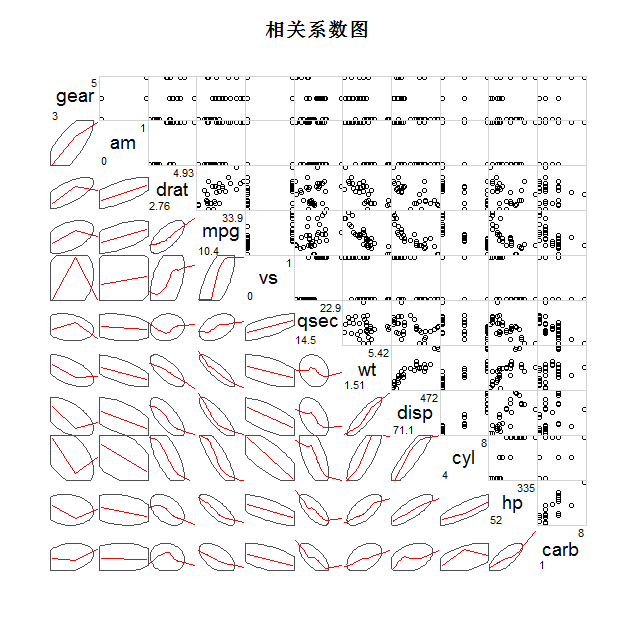
3、相关图
|
|

|
|
4、马赛克图
|
|
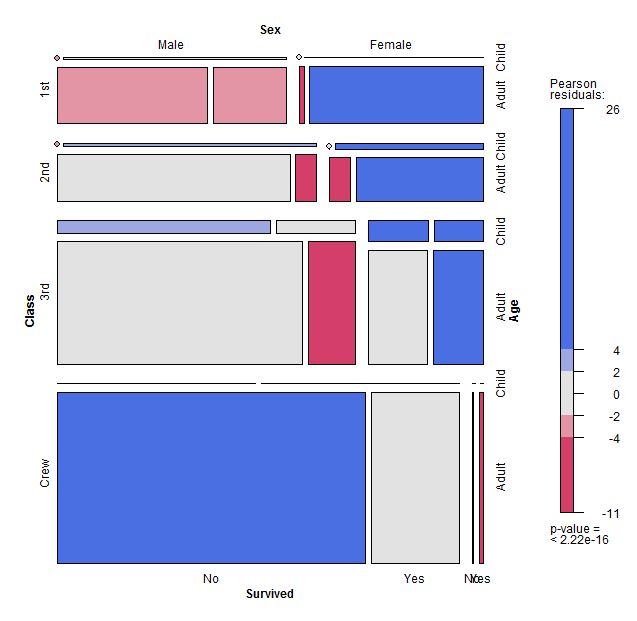
|
|

|
|

|
|


|
|


|
|

|
|

|
|

|
|

|
|

|
|

|
|

|
|

|
|

|
|

|
|



|
|

|
|

|
|

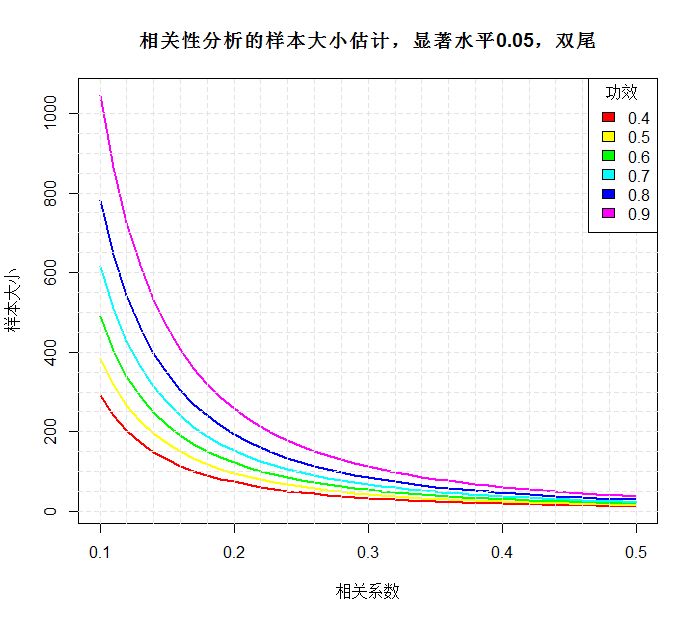
功效分析就是给定三个值得情况下,求得另外一个值
|
|
|
|
效应值f计算公式:
|
|
效应值f2计算公式:
|
|
|
|
|
|
加锁状态的读、更新或删除操作一般会将其扫描到的每一个索引的记录进行加锁,它并不关心where条件是否会包含这些行,InnoDB不记得具体的where条件,仅仅知道扫描了哪些索引区间,这种锁就是通常的next-key锁,其同时封锁了在此记录之前的区间插入(gap锁)。gap锁可以被禁用,这将导致next-key锁不再使用,事务的隔离级别也会影响加锁。
如果一个二级索引用在一个查询上,并且索引记录加了排它锁,InnoDB同时也睡将相应的聚簇索引记录加锁
如果没有合适的索引用于你的语句,MySQL必须扫描全表,则每一行都会被加锁,这样锁住了其他所有用户的插入,创建合适的索引非常重要。
对于SELECT ... FOR UPDATE或者SELECT ... LOCK IN SHARE MODE来说,其将锁加在扫描到的行上,并且在这些扫描到的行中那些不匹配结果的行(不符合where条件)会去释放锁,但是在一些情况下,这些行不会立即释放锁,因为最后的结果行和之前的原始行之间的联系在查询过程中丢失了,比如,在UNION中,扫描到的行插入了临时表进而再判断是否符合要求,这种情况下,原始的行在查询完成后锁才会释放。
InnoDB的加锁方式
SELECT ... FROM: 快照读,不加锁,除非事务的隔离级别设置为SERIALIZABLE,这种情况下查询在其查询到的记录索引上加next-key锁,如果查询通过唯一索引查询唯一的一行,则对该索引加记录锁。SELECT ... FROM ... LOCK IN SHARE MODE: 对所有查询到的记录加共享的next-key锁,如果查询通过唯一索引查询唯一的一行,则对该索引加记录锁。SELECT ... FROM ... FOR UPDATE: 对查询到的每一条记录设置排他的next-key锁,如果查询通过唯一索引查询唯一的一行,则对该索引加记录锁。对于查询到的记录,其还会在其他会话进行确定事务隔离级别的SELECT ... FROM ... LOCK IN SHARE MODEUPDATE ... WHERE ...: 记录添加排他的next-key锁,如果查询通过唯一索引查询唯一的一行,则对该索引加记录锁。DELETE FROM ... WHERE ...: 所有扫描到的记录加排他next-key锁,如果查询通过唯一索引查询唯一的一行,则对该索引加记录锁。INSERT对插入的行加排他锁,是记录锁而不是next-key锁,不锁区间如果在INSERT过程中,重复索引错误发生(duplicate-key error),则对这个重复的索引记录添加共享锁,此时可能发生死锁当多个会话试图插入同一行而另一个会话已经拥有一个排它锁时,这在删除该行时会发生。
|
|
INSERT ... ON DUPLICATE KEY UPDATE: 与insert的区别是在发生duplicate-key错误时,加的是排他的next-key锁
REPLACE: 类似没有唯一索引冲突的INSERT,另外当更新成功时候,行上加排他next-key锁。INSERT INTO T SELECT ... FROM S WHERE ...: 对插入到T中的每一行加排他记录锁,如果事务的隔离级别是RC,或者innodb_locks_unsafe_for_binlog启用并且隔离级别不是序列化,Innodb将S上的查询当作一个快照读,此时没有锁,否则,S上查询到的每一行加共享的next-key锁。CREATE TABLE ... SELECT ...: 类似上一个,只处理select部分的锁。REPLACE INTO t SELECT ... FROM s WHERE ...或UPDATE t ... WHERE col IN (SELECT ... FROM s ...):InnoDB对s上的记录加共享的next-key锁。