By

创建数据集

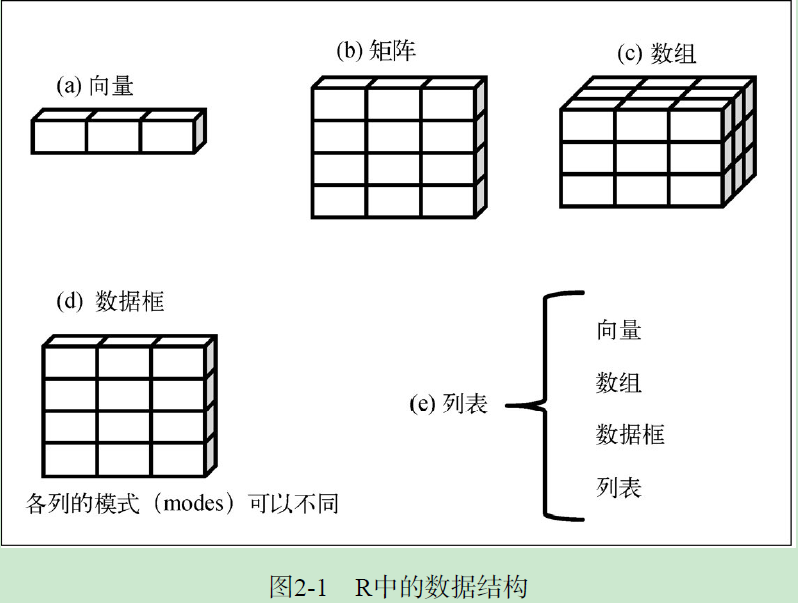
1. 向量

1
2
a<-c(1,2,3,4,5);b<-c("one","two","three")
cc<-c(TRUE,FALSE,TRUE)
  • 单个向量的数据类型必须一致

2. 标量

只含一个元素的向量：f<-3

3. 向量的访问：

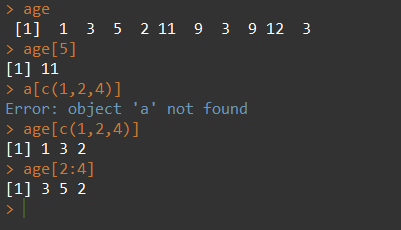
4. 矩阵

矩阵每个元素相同的模式

5. 数组：

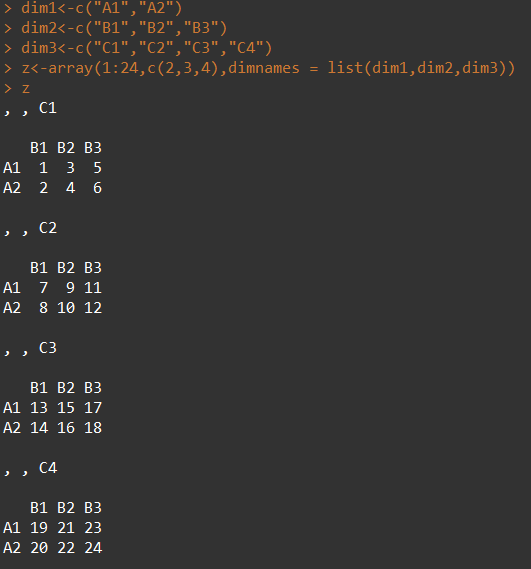
6. 数据框

最常用的数据结构，可以包含不同的数据模式（数据类型）
mydaya <- data.frame(col1,col2,col3),col1~col3可以为任何类型

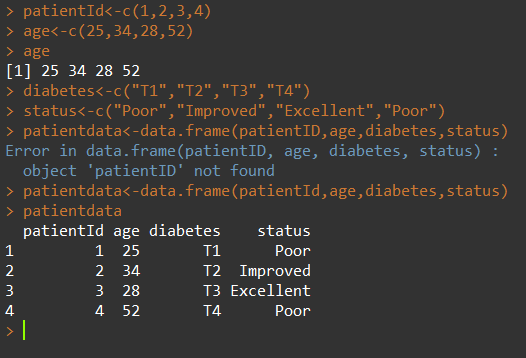
数据框变量内容的读取：

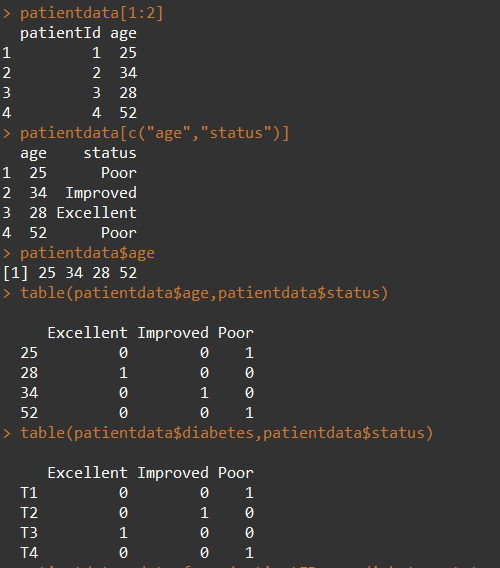
其中，变量名可以进行局部化：

1
2
3
4
5
6
7
8
attach(patientData)
table(diabetes,age)#此处直接可以使用
detach()#移除搜索路径
with(patientData,{
data1<- table(diabetes,age)
data2<<- table(diabetes,age)
})#单行可以直接写语句不需要大括号, 但普通方式赋值的变量外部无法使用，<<-可以外部使用

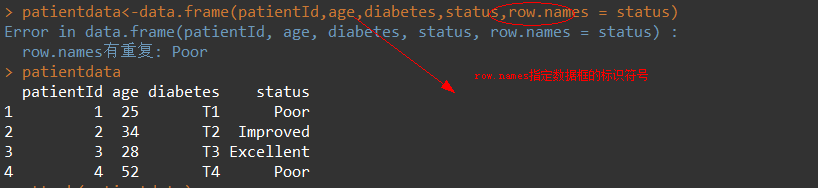
7. 因子

变量可归结为名义型、有序型或连续型变量，
  • 名义型-无顺序(类别标识，男，女)-因子
  • 有序型-有递进顺序，但不连续(病情的情况，好转，一般，差)-因子
  • 连续型-有顺序的任意范围内值(年龄) 


1
2
str(pData)#显示数据的结构
summary(pData)#显示简要的描述性统计

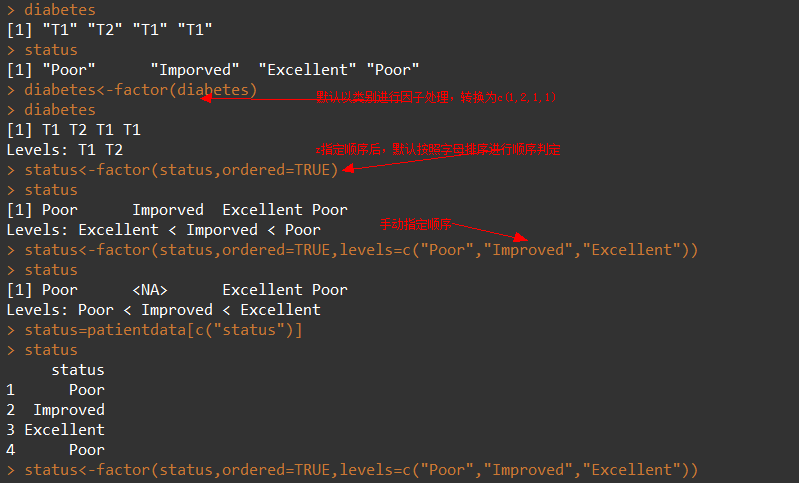
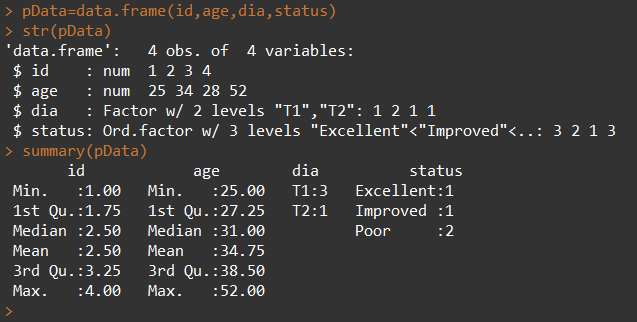
8. 列表

对象的有序集合，可以为任意对象：

1
2
list<-list(o1,…,o2)
list<-list(name1=o1,…,name2=o2)

9. 自动扩展特性

将一个值赋给某个向量、矩阵、数组或列表中一个不存在的元素时， R将自动扩展这个数据结构以容纳新值。

10. 删除变量

rm(var1)

11. 导入csv:

1
2
3
read.csv("area.csv",header = TRUE, sep=",", row.names="ID")
read.table("area.csv",header = TRUE, sep=",", row.names="ID")
fread("finaldata.csv", integer64="numeric", na.strings=c("NULL","NA", "", "\\N"))

12. 变量标签与值标签


13. 实用函数

  • length(object) 显示对象中元素/成分的数量
  • dim(object) 显示某个对象的维度
  • str(object) 显示某个对象的结构
  • class(object) 显示某个对象的类或类型
  • mode(object) 显示某个对象的模式
  • names(object) 显示某对象中各成分的名称
  • c(objectt,…) 将对象合并入一个向量
  • cbind(object,…) 按列合并对象
  • rbind(object, …) 按行合并对象
  • Object 输出某个对象
  • head(object) 列出某个对象的开始部分
  • tail(object) 列出某个对象的最后部分
  • ls() 显示当前的对象列表
  • rm(object, …) 删除一个或更多个对象。语句rm(list = ls())将删除当前工作环境中的几乎所有对象
  • newobject <- edit(object) 编辑对象并另存为newobject fix(object) 直接编辑对象

By

初窥

  1. c()函数，输入向量，x <- c(1,2,3,4,5)

  2. 帮助函数：

  3. 工作空间：

  4. 输入输出：sink(“filename”,append=TRUE,split=TRUE),将程序的输出定向至文件中，append表示追加，split表示是否同时在屏幕与文件同时输出，不加参数sink()仅指向屏幕，并且释放文件句柄。

  5. 图形输出使用以下命令：dev.off()释放文件句柄并将输出返回终端。

  6. .libPaths()显示库所在的位置; library()显示库中有哪些包。Search()显示那些包已经加载

  7. 包的管理

    • install.packages("xxx") 安装包
    • update.packages() 更新包
    • installed.packages() 已安装的包
    • library(gclus) 载入包
    • help(package="xx") 查看包的信息与函数

By

方差分析

  • 当包含的因子是解释变量时，我们关注的重点通常会从预测转向组别差异的分析，这种分析法称作方差分析 （ANOVA）。

    1、术语

  • 均衡/非均衡设计：不同观测方案的观测数相同/不同
  • 单因素方差分析：仅有一个类别型变量，一般为组间两水平因子（两种药物）
  • 单因素组内方差分析：仅有一个类型形变量，一般为组内两水平因子（同种药物，作用时间不同）
  • 因素方差分析：设计包含两个甚至更多的因子
  • 混合模型方差分析：因子设计包括组内和组间因子
  • 混淆因素/干扰因子：你不关心的因素，但其能解释你关心的组间差异
  • 协方差分析（ANCOVA）：度量并将混淆因子作为协变量考虑在模型中的方差分析
  • 多元方差分析（MANOVA）：因变量不止一个
  • 多元协方差分析（MANCOVA）：因变量不止一个的协方差分析

2、ANOVA模型拟合

  • lm函数与aov函数都可以分析方差分析模型，ANOVA和回归本质上都属于广义线性模型

    2.1、aov()函数

1
2
aov(formula, data = dataframe)
#formula可使用的参数符号见回归（一）

一些常见的研究设计表达式：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
#单因素ANOVA
y ~ A
#含单个协变量的单因素ANCOVA 
y ~ x + A
#双因素ANOVA 
y ~ A * B
#含两个协变量的双因素ANCOVA 
y ~ x1 + x2 + A*B
#随机化区组 
y ~ B + A（B是区组因子）
#单因素组内ANOVA  Subject标识一个独特的被试者
y ~ A + Error(Subject/A)
#含单个组内因子（W）和单个组间因子（B）的重复测量ANOVA 
y ~ B * W + Error(Subject/W)

2.2、顺序很重要

  • 例如，对于双因素方差分析，不同的处理方式观测数不同，则y~AB与y~BA结果不同

假设你正使用如下表达式对数据进行建模：

  • Y ~ A + B + A:B

有三种类型的方法可以分解等式右边各效应对y所解释的方差。

  • 类型I（序贯型）：效应根据表达式中先出现的效应做调整。 A不做调整， B根据A调整， A:B交互项根据A和B调整。
  • 类型II（分层型）：效应根据同水平或低水平的效应做调整。 A根据B调整， B依据A调整，A:B交互项同时根据A和B调整。
  • 类型III（边界型）：每个效应根据模型其他各效应做相应调整。 A根据B和A:B做调整， A:B交互项根据A和B调整。

样本大小越不平衡，效应项的顺序对结果的影响越大。一般来说，越基础性的效应越需要放在表达式前面。具体来讲，首先是协变量，然后是主效应，接着是双因素的交互项，再接着是三因素的交互项，以此类推。

  • R默认调用类型I方法，其他软件（比如SAS和SPSS）默认调用类型III方法。
  • car包中的Anova()函数（不要与标准anova()函数混淆）提供了使用类型II或类型III方法的选项。

3、单因素方差分析

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
> #单因素方差分析
> library(multcomp)
> attach(cholesterol)
The following objects are masked from cholesterol (pos = 4):
    response, trt
> table(trt)#各组样本大小
trt
 1time 2times 4times  drugD  drugE 
    10     10     10     10     10 
> aggregate(response,by=list(trt),FUN=mean)#计算response的均值
  Group.1        x
1   1time  5.78197
2  2times  9.22497
3  4times 12.37478
4   drugD 15.36117
5   drugE 20.94752
> aggregate(response,by=list(trt),FUN=sd)#计算response的标准差
  Group.1        x
1   1time 2.878113
2  2times 3.483054
3  4times 2.923119
4   drugD 3.454636
5   drugE 3.345003
> fit<-aov(response~trt)
> summary(fit)
            Df Sum Sq Mean Sq F value   Pr(>F)    
trt          4 1351.4   337.8   32.43 9.82e-13 ***
Residuals   45  468.8    10.4                     
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
> #ANOVA对治疗方式（trt）的F检验非常显著（p<0.0001），说明五种疗法的效果不同
> library(gplots)
> 
> #图形展示了带有95%的置信区间的各疗法均值，可以清楚看到它们之间的差异
> plotmeans(response~trt, xlab="Treatment", ylab="Response", main="Mean Plot")
> detach(cholesterol)

3.1、多重比较

1
2
3
4
5
TukeyHSD(fit)
par(las=2)
par(mar=c(5,8,4,2))
plot(TukeyHSD(fit))
#图形中置信区间包含0的疗法说明差异不显著（p>0.05）。

1
2
3
4
5
library(multcomp)
par(mar=c(5,4,6,2))
tuk<-glht(fit,linfct=mcp(trt="Tukey"))
plot(cld(tuk, level = .05),col="lightgrey")
#有相同字母的组差异不显著，图中，1time和2times差异不显著，1time和4times差异显著

3.2、检验的假设条件

  • 样本随机独立
  • 因变量的正态性
1
2
3
#单因素方差分析中，我们假设因变量服从正态分布，各组方差相等。可以使用Q-Q图来检验正态性假设
library(car)
qqPlot(lm(response~trt,data=cholesterol),simulate=TRUE,main="Q-Q Plot", labels=FALSE)

  • 样本的方差齐性（总体方差相等）

注意：F检验对于数据的正态性非常敏感，因此在检验方差齐性的时候，Levene检验, Bartlett检验或者Brown–Forsythe检验的稳健性都要优于F检验。 F检验还可以用于三组或者多组之间的均值比较，但是如果被检验的数据无法满足均是正态分布的条件时，该数据的稳健型会大打折扣，特别是当显著性水平比较低时。但是，如果数据符合正态分布，而且alpha值至少为0.05，该检验的稳健型还是相当可靠的。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
#Bartlett检验
> bartlett.test(response~trt,data=cholesterol)
	Bartlett test of homogeneity of variances
data:  response by trt
Bartlett K-squared = 0.57975, df = 4,
p-value = 0.9653
#Bartlett检验表明五组的方差并没有显著不同（p=0.97）。
#方差齐性分析对离群点非常敏感
> fit<-aov(response~trt)
> outlierTest(fit) #识别离群
No Studentized residuals with Bonferonni p < 0.05
Largest |rstudent|:
   rstudent unadjusted p-value Bonferonni p
19 2.251149           0.029422           NA
#从输出结果来看，并没有证据说明胆固醇数据中含有离群点（当p>1时将产生NA） 。

4、协方差分析

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
> #协方差分析
> #怀孕小鼠分组接收不同剂量药物，因变量幼崽体重，协变量怀孕时间
> data(litter,package = "multcomp")
> attach(litter)
The following objects are masked from litter (pos = 4):
    dose, gesttime, number, weight
> table(dose)
dose
  0   5  50 500 
 20  19  18  17 
> aggregate(weight,by=list(dose),FUN=mean)#计算weight的均值
  Group.1        x
1       0 32.30850
2       5 29.30842
3      50 29.86611
4     500 29.64647
> 
> fit<-aov(weight~gesttime+dose)
> summary(fit)
            Df Sum Sq Mean Sq F value  Pr(>F)   
gesttime     1  134.3  134.30   8.049 0.00597 **
dose         3  137.1   45.71   2.739 0.04988 * 
Residuals   69 1151.3   16.69                   
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
> #我们得到：(a)怀孕时间与幼崽出生体重相关； (b)控制怀孕时间，药物剂量与出生体重相关。
> 
> #去除协变量效应后的组均值
> library(effects)
> effect("dose",fit)
 dose effect
dose
       0        5       50      500 
32.35367 28.87672 30.56614 29.33460 
> 
> #multcomp包校验用户自定义的均值假设
> library(multcomp)
> #c(3, -1, -1, -1)设定第一组和其他三组的均值进行比较
> contrast<-rbind("no drug vs. drug"=c(3,-1,-1,-1))
> summary(glht(fit,linfct=mcp(dose=contrast)))
	 Simultaneous Tests for General Linear Hypotheses
Multiple Comparisons of Means: User-defined Contrasts
Fit: aov(formula = weight ~ gesttime + dose)
Linear Hypotheses:
                      Estimate Std. Error t value Pr(>|t|)  
no drug vs. drug == 0    8.284      3.209   2.581    0.012 *
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Adjusted p values reported -- single-step method)
> #可以得出未用药组比其他用药条件下的出生体重高的结论

4.1、检验的假设条件

1
2
3
4
5
6
7
8
9
10
11
12
13
> #假设条件
> #正态性和同方差性同方差分析
> #回归斜率相同
> fit2<-aov(weight~gesttime*dose,data = litter)
> summary(fit2)
              Df Sum Sq Mean Sq F value  Pr(>F)   
gesttime       1  134.3  134.30   8.289 0.00537 **
dose           3  137.1   45.71   2.821 0.04556 * 
gesttime:dose  3   81.9   27.29   1.684 0.17889   
Residuals     66 1069.4   16.20                   
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
> #可以看到交互效应不显著，支持了斜率相等的假设。

4.2、可视化

1
2
3
4
5
#可视化
library(HH)
ancova(weight~gesttime+dose,data=litter)
#可以看到，用怀孕时间来预测出生体重的回归线相互平行，只是截距项不同。随着怀
#孕时间增加，幼崽出生体重也会增加。另外，还可以看到0剂量组截距项最大， 5剂量组截距项最小。

5、双因素方差分析

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
> #双因素方差分析
> attach(ToothGrowth)
The following objects are masked from ToothGrowth (pos = 3):
    dose, len, supp
> table(supp,dose)
    dose
supp 0.5  1  2
  OJ  10 10 10
  VC  10 10 10
> aggregate(len,by=list(supp,dose),FUN=mean)
  Group.1 Group.2     x
1      OJ     0.5 13.23
2      VC     0.5  7.98
3      OJ     1.0 22.70
4      VC     1.0 16.77
5      OJ     2.0 26.06
6      VC     2.0 26.14
> aggregate(len,by=list(supp,dose),FUN=sd)
  Group.1 Group.2        x
1      OJ     0.5 4.459709
2      VC     0.5 2.746634
3      OJ     1.0 3.910953
4      VC     1.0 2.515309
5      OJ     2.0 2.655058
6      VC     2.0 4.797731
> fit<-aov(len~supp*dose)
> summary(fit)
            Df Sum Sq Mean Sq F value   Pr(>F)    
supp         1  205.4   205.4  12.317 0.000894 ***
dose         1 2224.3  2224.3 133.415  < 2e-16 ***
supp:dose    1   88.9    88.9   5.333 0.024631 *  
Residuals   56  933.6    16.7                     
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
> #可以看到主效应（supp和dose）和交互效应都非常显著
#可视化 推荐interaction2wt可展示双因素、三因素等
interaction2wt(len~supp*dose)

6、重复测量方差分析

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
> #重复测量方差分析
> #数据为不同浓度二氧化碳环境下两种植物对其的吸收量
> w1b1<-subset(CO2,Treatment=='chilled')
> fit<-aov(uptake~conc*Type+Error(Plant/conc),w1b1)
> summary(fit)
Error: Plant
          Df Sum Sq Mean Sq F value  Pr(>F)   
Type       1 2667.2  2667.2   60.41 0.00148 **
Residuals  4  176.6    44.1                   
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Error: Plant:conc
          Df Sum Sq Mean Sq F value   Pr(>F)    
conc       1  888.6   888.6  215.46 0.000125 ***
conc:Type  1  239.2   239.2   58.01 0.001595 ** 
Residuals  4   16.5     4.1                     
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Error: Within
          Df Sum Sq Mean Sq F value Pr(>F)
Residuals 30    869   28.97               
> 
> par(las=2)
> par(mar=c(10,4,4,2))
> with(w1b1,interaction.plot(conc,Type,uptake,type="b",col=c("red","blue"),pch = c(16,18),main=
+                              "植物类型和二氧化碳浓度的交互图"))
> boxplot(uptake~conc*Type,data=w1b1,col=(c("gold","green")),main="魁北克与密西西比植物对二氧化碳吸收的交互图")
> #魁北克省的植物比密西西比州的植物二氧化碳吸收率高，而且随着CO2浓度的升高，差异越来越明显。
> 
> #注意 该方法为传统的重复测量方差分析。该方法假设任意组内因子的协方差矩阵为球形，并且任意组内因子两水平间的方差之差都相等。


7、多元方差分析

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
> #研究美国谷物中的卡路
> #里、脂肪和糖含量是否会因为储存架位置的不同而发生变化。其中1代表底层货架， 2代表中层货
> #架， 3代表顶层货架。卡路里、脂肪和糖含量是因变量，货架是三水平（1、 2、 3）的自变量。
> library(MASS)
> attach(UScereal)
The following objects are masked from UScereal (pos = 7):
    calories, carbo, fat, fibre, mfr, potassium, protein, shelf, sodium, sugars, vitamins
The following objects are masked from UScereal (pos = 9):
    calories, carbo, fat, fibre, mfr, potassium, protein, shelf, sodium, sugars, vitamins
> y<-cbind(calories,fat,sugars)
> aggregate(y,by=list(shelf),FUN=mean)
  Group.1 calories       fat    sugars
1       1 119.4774 0.6621338  6.295493
2       2 129.8162 1.3413488 12.507670
3       3 180.1466 1.9449071 10.856821
> fit<-manova(y~shelf)
> summary(fit)
          Df  Pillai approx F num Df den Df  Pr(>F)   
shelf      1 0.19594    4.955      3     61 0.00383 **
Residuals 63                                          
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
> 
> summary.aov(fit)#输出单变量结果
 Response calories :
            Df Sum Sq Mean Sq F value    Pr(>F)    
shelf        1  45313   45313  13.995 0.0003983 ***
Residuals   63 203982    3238                      
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
 Response fat :
            Df  Sum Sq Mean Sq F value   Pr(>F)   
shelf        1  18.421 18.4214   7.476 0.008108 **
Residuals   63 155.236  2.4641                    
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
 Response sugars :
            Df  Sum Sq Mean Sq F value  Pr(>F)  
shelf        1  183.34  183.34   5.787 0.01909 *
Residuals   63 1995.87   31.68                  
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

7.1、评估假设检验

  • 多元正太性
1
2
3
4
5
6
7
8
center<-colMeans(y)
n<-nrow(y)
p<-ncol(y)
cov<-cov(y)
d<-mahalanobis(y,center,cov)
coord<-qqplot(qchisq(ppoints(n),df=p),d,main="Q-Q Plot",ylab="Maalanobis D2")
abline(a=0,b=1)
identify(coord$x,coord$y,labels=row.names(UScereal))

  • 方差-协方差矩阵同质性

    暂时没找到合适的方法来进行检验

  • 多元离群点

    1
    2
    library(mvoutlier)
    aq.plot(y)

7.2、稳健多元方差分析

  • 多元正态性或方差-协方差同质性不满足或担心离群点时
  • rrcov包中Wilks.test(y.dataframe,x,method=”mcp”)
  • vegan包中的adonis()
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    #稳健多元方差分析
    library(MASS)
    attach(UScereal)
    #稳健多元单因素方差分析
    library(rrcov)
    y<-cbind(calories,fat,sugars)
    Wilks.test(y,shelf,method="mcd")#性能较慢
    #非参数多元方差分析
    library(vegan)
    adonis(y~shelf)

8、用回归做ANOVA

  • 当lm()函数碰到因子时，它会用一系列与因子水平相对应的数值型对照变量来代替因子。（s1,s2,s3=>(0,0,0),(0,1,0),(0,0,1)）
创建方法 描述
contr.helmert 第二个水平对照第一个水平，第三个水平对照前两个的均值，第四个水平对照前三个的均值，以此类推
contr.poly 基于正交多项式的对照，用于趋势分析（线性、二次、三次等）和等距水平的有序因子
contr.sum 对照变量之和限制为0。也称作偏差找对，对各水平的均值与所有水平的均值进行比较
contr.treatment 各水平对照基线水平（默认第一个水平）。也称作虚拟编码
contr.SAS 类似于contr.treatment，只是基线水平变成了最后一个水平。生成的系数类似于大部分SAS过程中使用的对照变量
  • fit.lm <- lm(response ~ trt, data=cholesterol, contrasts=”contr.SAS”)的contrasts参数来改变创建方法，默认的创建方法为contr.treatment) 
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    > ##使用回归进行方差分析
    > library(multcomp)
    > levels(cholesterol$trt)
    [1] "1time"  "2times" "4times" "drugD"  "drugE" 
    > fit.aov <- aov(response ~ trt, data=cholesterol)
    > summary(fit.aov)
                Df Sum Sq Mean Sq F value   Pr(>F)    
    trt          4 1351.4   337.8   32.43 9.82e-13 ***
    Residuals   45  468.8    10.4                     
    ---
    Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
    > 
    > fit.lm <- lm(response ~ trt, data=cholesterol)
    > summary(fit.lm) #二者一致
    Call:
    lm(formula = response ~ trt, data = cholesterol)
    Residuals:
        Min      1Q  Median      3Q     Max 
    -6.5418 -1.9672 -0.0016  1.8901  6.6008 
    Coefficients:
                Estimate Std. Error t value Pr(>|t|)    
    (Intercept)    5.782      1.021   5.665 9.78e-07 ***
    trt2times      3.443      1.443   2.385   0.0213 *  
    trt4times      6.593      1.443   4.568 3.82e-05 ***
    trtdrugD       9.579      1.443   6.637 3.53e-08 ***
    trtdrugE      15.166      1.443  10.507 1.08e-13 ***
    ---
    Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
    Residual standard error: 3.227 on 45 degrees of freedom
    Multiple R-squared:  0.7425,	Adjusted R-squared:  0.7196 
    F-statistic: 32.43 on 4 and 45 DF,  p-value: 9.819e-13