By

广义线性模型

1、广义线性模型和glm函数、logistics回归

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
> #使用glm函数进行处理，可以分析多种分布，二分，多值，数值等，此处不限制因变量Y为服从正态分布
> #Logistic回归
> 
> library(AER)
> data("Affairs",package = "AER")
> summary(Affairs)
    affairs          gender         age         yearsmarried    children  religiousness  
 Min.   : 0.000   female:315   Min.   :17.50   Min.   : 0.125   no :171   Min.   :1.000  
 1st Qu.: 0.000   male  :286   1st Qu.:27.00   1st Qu.: 4.000   yes:430   1st Qu.:2.000  
 Median : 0.000                Median :32.00   Median : 7.000             Median :3.000  
 Mean   : 1.456                Mean   :32.49   Mean   : 8.178             Mean   :3.116  
 3rd Qu.: 0.000                3rd Qu.:37.00   3rd Qu.:15.000             3rd Qu.:4.000  
 Max.   :12.000                Max.   :57.00   Max.   :15.000             Max.   :5.000  
   education       occupation        rating     
 Min.   : 9.00   Min.   :1.000   Min.   :1.000  
 1st Qu.:14.00   1st Qu.:3.000   1st Qu.:3.000  
 Median :16.00   Median :5.000   Median :4.000  
 Mean   :16.17   Mean   :4.195   Mean   :3.932  
 3rd Qu.:18.00   3rd Qu.:6.000   3rd Qu.:5.000  
 Max.   :20.00   Max.   :7.000   Max.   :5.000  
> Affairs$ynAffair[Affairs$affairs > 0 ] <- 1
> Affairs$ynAffair[Affairs$affairs == 0 ] <- 0
> 
> Affairs$ynAffair <- factor(Affairs$ynAffair, levels = c(0,1), labels = c("No", "Yes"))
> 
> table (Affairs$ynAffair)
 No Yes 
451 150 
> 
> fit.full <- glm(ynAffair ~ gender + age + yearsmarried + children + religiousness + education + occupation + rating, data=Affairs,family = binomial())
> summary(fit.full)
Call:
glm(formula = ynAffair ~ gender + age + yearsmarried + children + 
    religiousness + education + occupation + rating, family = binomial(), 
    data = Affairs)
Deviance Residuals: 
    Min       1Q   Median       3Q      Max  
-1.5713  -0.7499  -0.5690  -0.2539   2.5191  
Coefficients:
              Estimate Std. Error z value Pr(>|z|)    
(Intercept)    1.37726    0.88776   1.551 0.120807    
gendermale     0.28029    0.23909   1.172 0.241083    
age           -0.04426    0.01825  -2.425 0.015301 *  
yearsmarried   0.09477    0.03221   2.942 0.003262 ** 
childrenyes    0.39767    0.29151   1.364 0.172508    
religiousness -0.32472    0.08975  -3.618 0.000297 ***
education      0.02105    0.05051   0.417 0.676851    
occupation     0.03092    0.07178   0.431 0.666630    
rating        -0.46845    0.09091  -5.153 2.56e-07 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for binomial family taken to be 1)
    Null deviance: 675.38  on 600  degrees of freedom
Residual deviance: 609.51  on 592  degrees of freedom
AIC: 627.51
Number of Fisher Scoring iterations: 4
> 
> #去除不显著的因素后再次进行建模
> fit.some <- glm(ynAffair ~  age + yearsmarried +  religiousness +  rating, data=Affairs,family = binomial())
> summary(fit.some)
Call:
glm(formula = ynAffair ~ age + yearsmarried + religiousness + 
    rating, family = binomial(), data = Affairs)
Deviance Residuals: 
    Min       1Q   Median       3Q      Max  
-1.6278  -0.7550  -0.5701  -0.2624   2.3998  
Coefficients:
              Estimate Std. Error z value Pr(>|z|)    
(Intercept)    1.93083    0.61032   3.164 0.001558 ** 
age           -0.03527    0.01736  -2.032 0.042127 *  
yearsmarried   0.10062    0.02921   3.445 0.000571 ***
religiousness -0.32902    0.08945  -3.678 0.000235 ***
rating        -0.46136    0.08884  -5.193 2.06e-07 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for binomial family taken to be 1)
    Null deviance: 675.38  on 600  degrees of freedom
Residual deviance: 615.36  on 596  degrees of freedom
AIC: 625.36
Number of Fisher Scoring iterations: 4
> 
> #新模型的每个回归系数都非常显著（p<0.05）。由于两模型嵌套（fit.some是fit.full
> #的一个子集），你可以使用anova()函数对它们进行比较，对于广义线性回归，可用卡方检验。
> 
> anova(fit.some, fit.full, test = "Chisq")
Analysis of Deviance Table
Model 1: ynAffair ~ age + yearsmarried + religiousness + rating
Model 2: ynAffair ~ gender + age + yearsmarried + children + religiousness + 
    education + occupation + rating
  Resid. Df Resid. Dev Df Deviance Pr(>Chi)
1       596     615.36                     
2       592     609.51  4   5.8474   0.2108
> 
> #卡方值不显著，得知两种模型的解释度是一样的
> 
> #回归系数
> coef(fit.some)
  (Intercept)           age  yearsmarried religiousness        rating 
   1.93083017   -0.03527112    0.10062274   -0.32902386   -0.46136144 
> #在Logistic回归中，响应变量是Y=1的对数优势比（log）。回归系数含义是当其他预测变量不
> #变时，一单位预测变量的变化可引起的响应变量对数优势比的变化。
> 
> #由于对数优势比解释性差，你可对结果进行指数化：
> exp(coef(fit.some))
  (Intercept)           age  yearsmarried religiousness        rating 
    6.8952321     0.9653437     1.1058594     0.7196258     0.6304248 
> 
> #可以看到婚龄增加一年，婚外情的优势比将乘以1.106（保持年龄、宗教信仰和婚姻评定不
> #变）；相反，年龄增加一岁，婚外情的的优势比则乘以0.965。因此，随着婚龄的增加和年龄、宗
> #教信仰与婚姻评分的降低，婚外情优势比将上升。因为预测变量不能等于0，截距项在此处没有
> #什么特定含义。
> 
> #还可使用confint()函数获取系数的置信区间。例如， exp(confint(fit.reduced))
> #可在优势比尺度上得到系数95%的置信区间。
> exp(confint(fit.some))
Waiting for profiling to be done...
                  2.5 %     97.5 %
(Intercept)   2.1255764 23.3506030
age           0.9323342  0.9981470
yearsmarried  1.0448584  1.1718250
religiousness 0.6026782  0.8562807
rating        0.5286586  0.7493370
> 
> #以概率的方式思考比使用优势比更直观。使用predict()函数，你
> #可观察某个预测变量在各个水平时对结果概率的影响。
> 
> testData <- data.frame(rating=c(1,2,3,4,5), age=mean(Affairs$age), yearsmarried=mean(Affairs$yearsmarried),
+                        religiousness=mean(Affairs$religiousness))
> 
> testData$prob <- predict(fit.some, newdata = testData, type="response")
> 
> testData
  rating      age yearsmarried religiousness      prob
1      1 32.48752     8.177696      3.116473 0.5302296
2      2 32.48752     8.177696      3.116473 0.4157377
3      3 32.48752     8.177696      3.116473 0.3096712
4      4 32.48752     8.177696      3.116473 0.2204547
5      5 32.48752     8.177696      3.116473 0.1513079
> #其他不变情况下 评级从1到5 婚外情概率从0.53降低至0.15
> 
> testData2 <- data.frame(age=seq(17,57,10), rating=mean(Affairs$rating), yearsmarried=mean(Affairs$yearsmarried),
+                        religiousness=mean(Affairs$religiousness))
> 
> testData2$prob <- predict(fit.some, newdata = testData2, type="response")
> 
> #对比图 评级影响更大 更剧烈
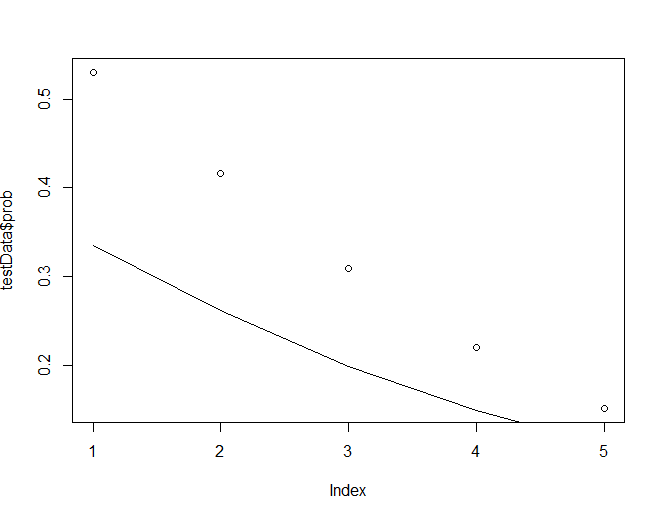
> plot(testData$prob)
> lines(testData2$prob)

2、logistics的过度离势

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
> #过度离势
> #过度离势，即观测到的响应变量的方差大于期望的二项分布的方差。过度离势会导致奇异的
> #标准误检验和不精确的显著性检验
> #出现过度离势时，仍可使用glm()函数拟合Logistic回归，但此时需要将二项分布改为类二
> #项分布（quasibinomial distribution）。
> #检测过度离势的一种方法是比较二项分布模型的残差偏差与残差自由度，比值大于1很多表示存在过度离势
> #婚外情中 模型中 Residual deviance: 615.36  on 596  degrees of freedom
> #残差615.36 和 残差自由度596 比值为1.03， 不存在过度离势
> 
> #也可使用检验法
> #为此，你需要拟合模型两次，第一次使用family =
> #  "binomial"，第二次使用family = "quasibinomial"。假设第一次glm()返回对象记为fit.1，
> #第二次返回对象记为fit.2，那么：
> fit.1 <- glm(ynAffair ~  age + yearsmarried +  religiousness +  rating, data=Affairs,family = binomial())
> 
> fit.2 <- glm(ynAffair ~  age + yearsmarried +  religiousness +  rating, data=Affairs,family = quasibinomial())
> 
> pchisq(summary(fit.2)$dispersion * fit.1$df.residual, fit.1$df.residual, lower = F)
[1] 0.340122
> #p值（0.34）显然不显著（p > 0.05），这更增强了我们认为不存在过度离势的信心。
> 
>

3、logistics的扩展

1
2
3
4
5
6
7
8
9
10
11
12
> #扩展
> 
> #稳健Logistic回归 robust包中的glmRob()函数可用来拟合稳健的广义线性模型，包
> #括稳健Logistic回归。当拟合Logistic回归模型数据出现离群点和强影响点时，稳健Logistic
> #回归便可派上用场。
> 
> #多项分布回归 若响应变量包含两个以上的无序类别（比如，已婚/寡居/离婚），便可使
> #用mlogit包中的mlogit()函数拟合多项Logistic回归。
> 
> #序数Logistic回归 若响应变量是一组有序的类别（比如，信用风险为差/良/好），便可
> #使用rms包中的lrm()函数拟合序数Logistic回归。
>

4、泊松回归

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
> #泊松回归
> #当通过一系列连续型和/或类别型预测变量来预测计数型结果变量时，泊松回归是一个非常
> #有用的工具。
> 
> data(breslow.dat, package="robust")
> 
> names(breslow.dat)
 [1] "ID"    "Y1"    "Y2"    "Y3"    "Y4"    "Base"  "Age"   "Trt"   "Ysum"  "sumY"  "Age10"
[12] "Base4"
> 
> summary(breslow.dat[c(6,7,8,10)])
      Base             Age               Trt          sumY       
 Min.   :  6.00   Min.   :18.00   placebo  :28   Min.   :  0.00  
 1st Qu.: 12.00   1st Qu.:23.00   progabide:31   1st Qu.: 11.50  
 Median : 22.00   Median :28.00                  Median : 16.00  
 Mean   : 31.22   Mean   :28.34                  Mean   : 33.05  
 3rd Qu.: 41.00   3rd Qu.:32.00                  3rd Qu.: 36.00  
 Max.   :151.00   Max.   :42.00                  Max.   :302.00  
> 
> 
> opar <- par(no.readonly = TRUE)
> 
> par(mfrow=c(1,2))
> attach(breslow.dat)
The following objects are masked from breslow.dat (pos = 4):
    Age, Age10, Base, Base4, ID, sumY, Trt, Y1, Y2, Y3, Y4, Ysum
> 
> hist(sumY, breaks = 20, xlab="Serzure Count", main="Distribution of Serzures")
> boxplot(sumY ~ Trt, xlab="Treatment", main="Group Comparisons")
> par(opar)


1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
> # 拟合泊松回归
> fit <- glm(sumY ~ Base + Age +Trt, data = breslow.dat, family = poisson())
> summary(fit)
Call:
glm(formula = sumY ~ Base + Age + Trt, family = poisson(), data = breslow.dat)
Deviance Residuals: 
    Min       1Q   Median       3Q      Max  
-6.0569  -2.0433  -0.9397   0.7929  11.0061  
Coefficients:
               Estimate Std. Error z value Pr(>|z|)    
(Intercept)   1.9488259  0.1356191  14.370  < 2e-16 ***
Base          0.0226517  0.0005093  44.476  < 2e-16 ***
Age           0.0227401  0.0040240   5.651 1.59e-08 ***
Trtprogabide -0.1527009  0.0478051  -3.194   0.0014 ** 
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for poisson family taken to be 1)
    Null deviance: 2122.73  on 58  degrees of freedom
Residual deviance:  559.44  on 55  degrees of freedom
AIC: 850.71
Number of Fisher Scoring iterations: 5
> 
> #泊松回归的因变量以条件均值的对数形式ln(λ)来建模，年龄的回归参数为0.0227，表明
> #保持其他预测变量不变，年龄增加一岁，癫痫发病数的对数均值将相应增加0.03。
> #指数化系数用于方便观察
> exp(coef(fit))
 (Intercept)         Base          Age Trtprogabide 
   7.0204403    1.0229102    1.0230007    0.8583864 
> #保持其他变量不变，年龄增加一岁，期望的癫痫发病数将乘以1.023。
> #与Logistic回归中的指数化参数相似，泊松模型中的指数化参数对响应
> #变量的影响都是成倍增加的，而不是线性相加。
>

5、泊松回归的过度离势

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
> #泊松分布的过度离势
> #泊松分布的方差和均值相等。当响应变量观测的方差比依据泊松分布预测的方差大时，泊松
> #回归可能发生过度离势。
> #与Logistic回归类似，此处如果残差偏差与残差自由度的比例远远大于1，那么表明存在过度
> #离势。559.44/55 >>1
> 
> #qcc包的一个方法可用于检测泊松模型的过度离势
> library(qcc)
> qcc.overdispersion.test(breslow.dat$sumY, type="poisson")
                   
Overdispersion test Obs.Var/Theor.Var Statistic p-value
       poisson data          62.87013  3646.468       0
> 
> #显著性检验的p值果然小于0.05，进一步表明确实存在过度离势
> 
> #此时仍可使用glm进行拟合
> fit.od <- glm(sumY ~ Base + Age +Trt, data = breslow.dat, family = quasipoisson())
> summary(fit.od)
Call:
glm(formula = sumY ~ Base + Age + Trt, family = quasipoisson(), 
    data = breslow.dat)
Deviance Residuals: 
    Min       1Q   Median       3Q      Max  
-6.0569  -2.0433  -0.9397   0.7929  11.0061  
Coefficients:
              Estimate Std. Error t value Pr(>|t|)    
(Intercept)   1.948826   0.465091   4.190 0.000102 ***
Base          0.022652   0.001747  12.969  < 2e-16 ***
Age           0.022740   0.013800   1.648 0.105085    
Trtprogabide -0.152701   0.163943  -0.931 0.355702    
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for quasipoisson family taken to be 11.76075)
    Null deviance: 2122.73  on 58  degrees of freedom
Residual deviance:  559.44  on 55  degrees of freedom
AIC: NA
Number of Fisher Scoring iterations: 5
> #注意，使用类泊松（quasi-Poisson）方法所得的参数估计与泊松方法相同，但标准误变大
> #了许多。此处，标准误越大将会导致Trt（和Age）的p值越大于0.05。当考虑过度离势，并控
> #制基础癫痫数和年龄时，并没有充足的证据表明药物治疗相对于使用安慰剂能显著降低癫痫发
> #病次数

By

重抽样与自助法

1、置换检验

1
2
3
4
5
6
7
8
> #置换方法并不是将统计量与理论分布进行比较，而是将其与置换观测数据后获得的经验分布进行比较，
> #根据统计量值的极端性判断是否有足够理由拒绝零假设。比如判断两组处理数据的内在差异性
> #将所有观测组数据混合后重新随机拆分至所有组合计算统计量如（t值），所有统计量升序排列，根据第一个统计量
> #（如t0）进行判断
> #置换检验真正发挥功用的地方是处理非正态数据（如分布偏倚很大）、存在离群点、
> #样本很小或无法做参数检验等情况。不过，如果初始样本对感兴趣的总体情况代表性很差，即使
> #是置换检验也无法提高推断效果。
> #置换检验主要用于生成检验零假设的p值，它有助于回答“效应是否存在”这样的问题。

2、使用coin包进行置换检验

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
#独立2样本检验和K样本检验
> library(coin)
> score <- c(40,57,45,55,58,57,64,55,62,65)
> treatment <- factor(c(rep("A",5), rep("B",5)))
> mydata <- data.frame(treatment, score)
> t.test(score~treatment, data=mydata,  var.equal = TRUE)
	Two Sample t-test
data:  score by treatment
t = -2.345, df = 8, p-value = 0.04705
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 -19.0405455  -0.1594545
sample estimates:
mean in group A mean in group B 
           51.0            60.6 
> #distribution = "exact"，那么在零假设条件下，分布的计算是精确的（即依据所有
> #可能的排列组合）,当前仅可用于两样本问题
> oneway_test(score~treatment, data=mydata,  distribution='exact')
	Exact Two-Sample Fisher-Pitman Permutation Test
data:  score by treatment (A, B)
Z = -1.9147, p-value = 0.07143
alternative hypothesis: true mu is not equal to 0
> 
> #测试美国南部与非南部的监禁概率
> library(MASS)
> UScrime <- transform(UScrime, So = factor(So))
> wilcox_test(Prob ~ So, data=UScrime, distribution="exact")
	Exact Wilcoxon-Mann-Whitney Test
data:  Prob by So (0, 1)
Z = -3.7493, p-value = 8.488e-05
alternative hypothesis: true mu is not equal to 0
> #监禁在南部可能更多
> 
> #K样本问题, 五种治疗方案的差异性,参考分布得自于数据9999次的置换
> library(multcomp)
> set.seed(1234)
> oneway_test(response ~ trt, data = cholesterol, distribution=approximate(B=9999))
	Approximative K-Sample Fisher-Pitman Permutation Test
data:  response by trt (1time, 2times, 4times, drugD, drugE)
chi-squared = 36.381, p-value < 2.2e-16
> 
> 
> #列联表中的独立性
> #检验两类别型变量的独立性
> library(coin)
> library(vcd)
> #转换治疗效果变量为分类因子，有序因子coin会生产一个线性与线性的趋势检验，而不是卡方检验
> Arthritis <- transform(Arthritis, Improved=as.factor(as.numeric(Improved)))
> set.seed(1234)
> chisq_test(Treatment ~ Improved, data=Arthritis, distribution=approximate(B=9999))
	Approximative Pearson Chi-Squared Test
data:  Treatment by Improved (1, 2, 3)
chi-squared = 13.055, p-value = 0.0018
> 
> 
> #两数值型变量的独立性置换检验，文盲率与谋杀率
> #转换为数据框，x77是一个矩阵
> states <- as.data.frame(state.x77)
> set.seed(1234)
> spearman_test(Illiteracy~Murder, data=states, distribution=approximate(B=9999))
	Approximative Spearman Correlation Test
data:  Illiteracy by Murder
Z = 4.7065, p-value < 2.2e-16
alternative hypothesis: true rho is not equal to 0
> 
> #两样本和K样本相关性检验
> library(coin)
> library(MASS)
> wilcoxsign_test(U1~U2, data=UScrime, distribution="exact")
	Exact Wilcoxon-Pratt Signed-Rank Test
data:  y by x (pos, neg) 
	 stratified by block
Z = 5.9691, p-value = 1.421e-14
alternative hypothesis: true mu is not equal to 0

3、ImPerm包置换检验

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
#ImPerm包 提供线性模型的置换方法，回归和方差分析
> #简单回归
> library(lmPerm)
> fit<-lmp(weight~height, data=women, perm="Prob")
[1] "Settings:  unique SS : numeric variables centered"
> summary(fit)
Call:
lmp(formula = weight ~ height, data = women, perm = "Prob")
Residuals:
    Min      1Q  Median      3Q     Max 
-1.7333 -1.1333 -0.3833  0.7417  3.1167 
Coefficients:
       Estimate Iter Pr(Prob)    
height     3.45 5000   <2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 1.525 on 13 degrees of freedom
Multiple R-Squared: 0.991,	Adjusted R-squared: 0.9903 
F-statistic:  1433 on 1 and 13 DF,  p-value: 1.091e-14 
> 
> #多项式回归
> library(lmPerm)
> set.seed(1234)
> fit<-lmp(weight ~ height + I(height^2), data = women, perm = "Prob")
[1] "Settings:  unique SS : numeric variables centered"
> summary(fit)
Call:
lmp(formula = weight ~ height + I(height^2), data = women, perm = "Prob")
Residuals:
      Min        1Q    Median        3Q       Max 
-0.509405 -0.296105 -0.009405  0.286151  0.597059 
Coefficients:
            Estimate Iter Pr(Prob)    
height      -7.34832 5000   <2e-16 ***
I(height^2)  0.08306 5000   <2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.3841 on 12 degrees of freedom
Multiple R-Squared: 0.9995,	Adjusted R-squared: 0.9994 
F-statistic: 1.139e+04 on 2 and 12 DF,  p-value: < 2.2e-16 
> 
> 
> #多元回归
> library(lmPerm)
> set.seed(1234)
> states <- as.data.frame(state.x77)
> fit <- lmp(Murder ~ Population + Illiteracy + Income + Frost, data=states, perm="Prob")
[1] "Settings:  unique SS : numeric variables centered"
> summary(fit)
Call:
lmp(formula = Murder ~ Population + Illiteracy + Income + Frost, 
    data = states, perm = "Prob")
Residuals:
     Min       1Q   Median       3Q      Max 
-4.79597 -1.64946 -0.08112  1.48150  7.62104 
Coefficients:
            Estimate Iter Pr(Prob)    
Population 2.237e-04   51   1.0000    
Illiteracy 4.143e+00 5000   0.0004 ***
Income     6.442e-05   51   1.0000    
Frost      5.813e-04   51   0.8627    
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 2.535 on 45 degrees of freedom
Multiple R-Squared: 0.567,	Adjusted R-squared: 0.5285 
F-statistic: 14.73 on 4 and 45 DF,  p-value: 9.133e-08 
> 
> #单因素方差分析
> library(lmPerm)
> library(multcomp)
> set.seed(1234)
> fit <- aovp(response~trt, data=cholesterol, perm="Prob")
[1] "Settings:  unique SS "
> summary(fit)
Component 1 :
            Df R Sum Sq R Mean Sq Iter  Pr(Prob)    
trt          4  1351.37    337.84 5000 < 2.2e-16 ***
Residuals   45   468.75     10.42                   
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
> 
> #单因素协方差分析
> library(lmPerm)
> set.seed(1234)
> fit <- aovp(weight ~ gesttime + dose, data=litter, perm="Prob")
[1] "Settings:  unique SS : numeric variables centered"
> summary(fit)
Component 1 :
            Df R Sum Sq R Mean Sq Iter Pr(Prob)    
gesttime     1   161.49   161.493 5000   0.0006 ***
dose         3   137.12    45.708 5000   0.0392 *  
Residuals   69  1151.27    16.685                  
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
> 
> #双因素方差分析
> library(lmPerm)
> set.seed(1234)
> fit <- aovp(len ~ supp * dose, data=ToothGrowth, perm="Prob")
[1] "Settings:  unique SS : numeric variables centered"
> summary(fit)
Component 1 :
            Df R Sum Sq R Mean Sq Iter Pr(Prob)    
supp         1   205.35    205.35 5000  < 2e-16 ***
dose         1  2224.30   2224.30 5000  < 2e-16 ***
supp:dose    1    88.92     88.92 2032  0.04724 *  
Residuals   56   933.63     16.67                  
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

4、自助法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
#boot包中的自助法，即通过一个函数重复执行多次取得统计量的序列分布
> #对单个统计量使用自助法
> rsq <- function(formula, data, indicates) {
+     d <- data[indicates,]
+     fit <- lm(formula, data=d)
+     return(summary(fit)$r.square)
+ }
> library(boot)
> set.seed(1234)
> results <- boot(data=mtcars, statistic = rsq, R=1000, formula=mpg~wt+disp)
> 
> print(results)
ORDINARY NONPARAMETRIC BOOTSTRAP
Call:
boot(data = mtcars, statistic = rsq, R = 1000, formula = mpg ~ 
    wt + disp)
Bootstrap Statistics :
     original    bias    std. error
t1* 0.7809306 0.0133367  0.05068926
> plot(results)
#置信区间都不包含R平方值0，所以拒绝零假设
> boot.ci(results, type=c("perc", "bca"))
BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
Based on 1000 bootstrap replicates
CALL : 
boot.ci(boot.out = results, type = c("perc", "bca"))
Intervals : 
Level     Percentile            BCa          
95%   ( 0.6838,  0.8833 )   ( 0.6344,  0.8549 )  
Calculations and Intervals on Original Scale
Some BCa intervals may be unstable
>

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
> #多个统计量自助法
> bs <- function(formula, data, indices) {
+   d <- data[indices,]
+   fit <- lm(formula, data=d)
+   return(coef(fit))
+ }
> 
> library(boot)
> set.seed(1234)
> results <- boot(data=mtcars, statistic = bs, R=1000, formula=mpg~wt+disp)
> 
> print(results)
ORDINARY NONPARAMETRIC BOOTSTRAP
Call:
boot(data = mtcars, statistic = bs, R = 1000, formula = mpg ~ 
    wt + disp)
Bootstrap Statistics :
       original        bias    std. error
t1* 34.96055404  0.1378732942 2.485756673
t2* -3.35082533 -0.0539040965 1.170427539
t3* -0.01772474 -0.0001208075 0.008786803
> #查看车重的抽样结果
> plot(results, index=2)
> #查看车重的95置信区间
> boot.ci(results, type= "bca", index=2)
BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
Based on 1000 bootstrap replicates
CALL : 
boot.ci(boot.out = results, type = "bca", index = 2)
Intervals : 
Level       BCa          
95%   (-5.655, -1.194 )  
Calculations and Intervals on Original Scale
> #查看排量的95置信区间
> boot.ci(results, type= "bca", index=3)
BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
Based on 1000 bootstrap replicates
CALL : 
boot.ci(boot.out = results, type = "bca", index = 3)
Intervals : 
Level       BCa          
95%   (-0.0331,  0.0010 )  
Calculations and Intervals on Original Scale

By

内存模型与并发

1 内存模型

1.1 硬件层面的缓存一致性

  • CPU核心、高速缓存与主内存之间通过缓存一致性协议保持数据的版本问题

    1.2 Java内存模型

    1.2.1 Java内存模型概述

  • 每个线程拥有自己的工作内存，不同线程间的工作内存不可见，线程所有操作都操作工作内存
  • 工作内存与主内存之间的数据同步通过定义的一些原子操作实现（lock、unlock、read、load、use、assign（赋值）、store、write）（1.5之后不再使用这种方式描述内存模型，使用先行发生原则）

    1.2.2 volatile变量

  • volatile只保证可见性，并非线程安全，多线程仍然会出现不安全的
  • 运算结果不依赖当前volatile变量或不需要与其他变量共同参与不变约束时，推荐使用volatile
  • volatile禁止指令重排序，线程内表现为串行

    1.2.3 long与double

  • Java内存模型不保证64位数据类型的load、store、read、write 4个操作的原子性，long与double的非原子性协定，但现在的虚拟机已经实现原子性

    1.2.4 原子性、可见性与有序性

  • 原子性：字节码monitorenter与monitorexit实现（管程）
  • 可见性：新值同步主存，读取从主存刷新方式实现，另外，volatile保证新值立即同步主存，读取时立即从内存刷新，synchronized块中，对一个变量执行unlock之前必须刷回主存，final保证一单初始化完成，其他线程立即可见
  • 有序性：线程内观察，所有操作有序，观察其他线程，所有操作无序（线程内表现为串行语义；指令重排序与工作内存与主存的差异）

1.2.5 先行发生原则

  • Java内存模型中存在天然的先后操作顺序，无需同步措施，如果两个操作不属于这些规则，则不保证顺序性
  • 先行发生原则：
    • 程序次序： 最终按照代码顺序执行
    • 管程锁定： unlock操作先于同一个锁的后一个lock操作（时间的先后）
    • volatile变量：对一个volatile变量的写先于后面的读（时间的先后）
    • 线程启动： Thread的start先于线程的每一个动作
    • 线程终止： 线程中的左右操作都先于对该线程的终止检测
    • 线程中断： 对线程interrupt()方法的调用先于被中断线程的代码检测到中断事件的发生
    • 对象终结： 一个对象的初始化完成先于finalize()方法
    • 传递性： A先于B，B先于C，A先于C
  • 一个操作时间上的先发生不代表该操作先行发生

1.3 Java与线程

1.3.1 线程的实现

  • 使用内核线程实现：程序使用轻量级进程LWP（内核线程的高级接口）进行线程映射，每个轻量级进程对应一个内核线程，这种1:1的关系成为一对一的线程模型，线程的所有操作需要进行系统调用，需要用户态和内核态进行切换，轻量级进程需要消耗一定的内核资源，一个系统支持的轻量级进程数量是有限的

  • 使用用户线程实现：系统内核不能感知用户线程的存在，其建立、同步、销毁和调度全在用户态完成，不需要内核的帮助，这种进程与用户线程的1:N的关系成为一对多的线程模型，难以实现，逐步放弃

  • 使用用户线程+LWP：以上两种结合推理

  • Java实现：Windows与Linux使用一对一线程模型实现，Windows与Linux提供的线程模型就是一对一的

1.3.2 线程调度

  • 协同式调度（协程）：线程主动通知系统切换线程，如Lua的协程，缺点执行时间不可控制，某个线程可能一直不通知
  • 抢占式调度：每个线程由系统来分配执行时间，Java采用，Java提供了10中线程的优先级来代表次序，但是Java的优先级不一定靠谱，有的OS提供的线程优先级不一致，如windows提供7种，无法与之一一对应，此外优先级可能被OS的各种优化与功能改变

1.3.3 状态转换

参见

2 线程安全与锁优化

2.1 线程安全

  • 多线程访问一个对象，不用考虑线程的调度与交替运行，也不需要进行额外的同步，调用这个对象的行为产生正确的结果

    2.1.1 Java的线程安全

  • Java的安全性：
    • 不可变
    • 绝对线程安全
    • 相对线程安全（单独的操作是线程安全的，但是对于特定的顺序连续调用，需要额外的同步手段，如Vector的读取与删除同时进行）
    • 线程兼容（对象不是线程安全，可以使用同步手段达到线程安全）
    • 线程对立（无法在多线程环境运行，Threadsuspend()、Thread.resume()可能引发死锁）

2.1.2 Java的线程安全的实现方法

  • 互斥同步：synchronized关键字实现，字节码指令对应monitorenter与monitorexit,这两个字节码需要一个reference类型参数，如果Java代码未指定，则为对象实例或Class对象，进入该指令时，首先要获取对象的锁，如果当前线程已经获取则将计数器+1，线程可重入，不会锁死自己，由于该语句会导致线程状态切换，线程需要进入核心态，消耗较大

    • 也可以使用ReentrantLock，性能更好, 但1.6之后synchronized关键字的吞吐量已经大幅提高，推荐使用原生synchronized关键字（1.8 ConcurrentHashMap源码已经使用synchronized来实现，Doug lea已经认可了synchronized的性能）

  • 非阻塞同步：CAS指令，需要硬件指令集支持（比较和更新需要原子操作），需要三个参数，内存位置，预期值，新值，Java中使用Unsafe类提供该操作

    • CAS指令会有ABA问题，可以使用AtomicStampedReference来控制变量的版本，更推荐使用互斥同步解决，因为一般ABA不影响并发的正确性。
    • 该类只支持Bootstrap ClassLoader加载，用户程序默认无法使用，只可以通过反射：
      1
      2
      3
      4
      5
      6
      7
      8
      9
      10
      11
      12
      13
      14
      15
      16
      17
      18
      19
      20
      21
      22
      23
      24
      25
      26
      27
      28
      29
      30
      31
      32
      33
      34
      35
      36
      37
      38
      /**
       * 一个简单的示例
       * Date: 2017/6/13
       * Time: 17:04
       */
      public class CasSample {
          public volatile long casVar;
          private static long CASVAR_OFFSET;
          static Unsafe unsafe;
          static {
              try {
                  Field field = Unsafe.class.getDeclaredField("theUnsafe");
                  field.setAccessible(true);
                  unsafe = (Unsafe) field.get(null);
                  Class<?> k = CasSample.class;
                  //取偏移量 实例变量使用objectFieldOffset，类静态变量使用staticFieldOffset
                  CASVAR_OFFSET = unsafe.objectFieldOffset(k.getField("casVar"));
              } catch (Exception e) {
                  e.printStackTrace();
              }
          }
          public static void main(String[] args) {
              CasSample casSample = new CasSample();
              casSample.casVar = 1;
              casSample.CAS_Swap();
          }
          private void CAS_Swap() {
              unsafe.compareAndSwapInt(this, CASVAR_OFFSET, 1, 2);
              System.out.println("cas" + casVar);
          }
      }

2.2 锁优化

  • JVM层面的优化

    2.2.1 自旋锁与自适应锁

  • 自旋锁：互斥同步线程阻塞不先不进入内核态挂起，而是让线程执行一个自旋，期待循环之后别的线程就可以释放锁了，自旋占用CPU时间，不可无限制自旋，自旋次数默认10
  • 自适应锁：自旋的时间不固定了，由前一次在同一个锁上的自旋时间以及锁拥有着的状态决定，比如上次自旋成功获得了锁A，当前持有锁的线程正在运行，虚拟机判断本次自旋获取到锁的可能性很大，进而自旋100次

2.2.2 锁消除

  • 自动判断当前代码块内是否会出现共享数据竞争，如果没有竞争，则将该段的同步措施去除。

2.2.3 锁粗化

  • 锁的使用通常要求锁的范围越小越好，但是若一系列的操作对同一个对象频繁的加锁解锁，比如出现在循环体内，那么这种加锁导致不必要的性能损耗，虚拟机探测到后会将同步措施放在整个操作序列的外部。

2.2.4 轻量级锁

  • 假设是对于绝大部分锁，整个同步周期内不存在竞争，根据对象头中的信息来表示对象的锁信息，参考

  • 如果对象没有被锁定，即锁标志位为01，则JVM在栈帧中创建一个锁记录的空间（Lock Record）,存储当前对象的Mark Word备份，CAS更新对象的Mark Word为Lock Record的指针，若成功，则表示该线程获得了锁，且锁标志位变为00，此时对象处于轻量级锁定状态、

  • 如果上述CAS失败，JVM检查该对象的Mark Word是否指向当前线程的栈帧，如果是则表示该线程已经获得锁，直接进入同步块执行，若失败，则锁膨胀为重量级锁，锁标志位变为10，Mark Word中存储重量级锁的指针（互斥量），后续等待线程进入阻塞状态

  • 解锁依然使用CAS，若Mark Word依然指向线程的锁记录，则CAS替换回来那份拷贝，成功则完毕，失败则表示锁定期间有其他线程尝试获取改锁（此时Mark Word指向的是互斥量），释放锁同时唤醒被挂起的线程

2.2.5 偏向锁

  • 据统计，在实际情况下，大部分的锁对象永远只被一个线程占用，轻量级锁在每次monitorenter和monitorexit的时候（非重入），都会进行一次cas操作，为了进一步减少cas操作，偏向锁（biased locking）诞生了。是否启用偏向锁由Mark Word中的一位表示，位于锁标记位前，可偏向为1
  • 锁对象第一次被线程获取，CAS将线程ID设置在Mark Word中，成功则该线程进入同步块时，不再进行任何同步操作
  • 另外一个线程获取锁时：
    1. 看一眼持有锁的线程是否还活着，如果已经死了，那将对象设置为无锁状态就可以了
    2. 如果这个线程还活着，那需要遍历持有这个锁的线程的栈帧中的所有lock record，如果所有lock record都不指向锁对象，那么这个线程实际上不持有这个对象锁。同1，将对象设置为无锁状态即可
    3. 如果这个线程正在占用这个锁对象，那么需要修改线程中的锁记录与对象头，将它们都修改为轻量级锁状态，然后正常走轻量级锁的流程即可，是否偏向锁标记位为0